排序算法

归并排序

归并排序是一种高效的基于比较的分治递归算法
合并排序在 𝑶𝑵𝐥𝐠𝑵 在最坏情况和平均情况下运行，算法使用的比较次数几乎是最优的

Merge sort runs in 𝑶 𝑵𝐥𝐠𝑵 both worst-case and average-case running time and the number of comparisons used by the algorithm is nearly optimal.

归并排序的许多实现是稳定的，即输入和输出中相等元素的顺序是相同的

归并排序：将待排序的元素序列分成两个子序列，每个子序列有N/2个元素

分而治之

归并排序算法遵循分而治之的范式，将问题划分为多个子问题，这些子问题是同一问题的较小实例
通过递归解决子问题来完成算法,将子问题的解组合成原问题的解

归并排序：对两个子序列进行递归排序,合并两个排序的子序列以产生排序的答案

1.Divide the problem into a number of subproblems that are smaller instances of the same problem
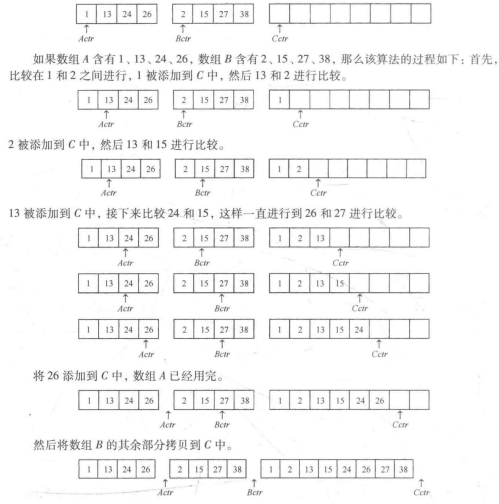
2.Conquer the subproblems by solving them recursively
3.Combine the solutions to the subproblems into the solution for the original problem

图解

在这个图解中，假设了A、B均是非递减数组，实质上在我们后面利用递归计算的时候，不用考虑传入数组的性质的

说白了，归并的核心步骤在于“从A/B数组中找到较小值并加入于C中”
另外，合并两个已排序的表的时间是线性的，这一点在算法分析的时候会用到

实现：书本实现

先谈谈书本的实现，个人认为更好理解而且适用性更高 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
//% 主要例程，mergeSort。其中public表达是驱动private方法的方式  
public static void mergeSort(AnyType [] a){
    AnyType[] tmpArray = (AnyType[]) new Comparable [a.length] ; 
    //事实上，这里的Comparable有可能成为后续开销的主要来源，见P197的解释

    mergeSort(a,tempArray,0,a.length-1);
}

//% mergeSort真正执行的方法 

/*
    一个目标数组a
    一个临时存储数组tempArray
    左右的端点left right
*/
private static void mergeSort(AnyType [] a , AnyType[] tempArray , int left , int right){
    if(left < right){
        //相等即完成
        int center = (left + right) / 2 ; 

        //分治之分，旨在对left和right两边进行再排序直到baseCase
        mergeSort(a,tempArray,left,center) ; 
        mergeSort(a,tempArray,center+1,right) ; 

        merge(a,tempArray,left,center+1,right) ; 
        //进行合并（“治”）的方法，见后
    }
}

//% merge 进行合并的方法

/*
    一个目标数组a
    一个临时存储数组tempArray
    左端点left
    右侧数组的起始点
*/
private static void merge(AnyType[] a , AnyType[] tempArray , int left , int rightPoint , int rightEnd){
    int leftEnd = rightPoint - 1 ;
    int temPos = left ; //结果数组的下标    
    int numElements = rightEnd - left + 1 ;//元素总数

    //主要进行填入的循环
    //核心思想：比较两个数组的最小值，填入二者中的较小者。一个数组填完之后就直接填另外一个数组所有的东西
    //这个步骤对于递归的每一步都是适用的    

    while(left <= leftEnd && rightPoint <= rightEnd ){
        if(a[left].compareTo(a[rightPoint]) <= 0 ){
            tempArray[temPos++] = a[left++];
        }else{
            tempArray[temPos++] = a[rightPoint++] ; 
        }
    }

        //
        while(left<=leftEnd){
            tempArray[temPos++] = a[left++] ; 
        }

        while(rightPoint <= rightEnd){
            tempArray[temPos++] = a[rightPoint++] ; 
        }

        //Copy数组，得到结果
        for(int i = 0 ; i < numElements ; i++){
            a[rightEnd] = tempArray[rightEnd] ; 
        }
        
}

实现：百度百科

这部分实现来自百度百科，几乎没有注释，仅仅作为补充
可以用以下代码，佐以递归，实现归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
mergeSort(data,left,right){
    if(left<right){
        center = (left+right)/2

        //归，分的过程
        mergeSort(data,left,center);
        mergeSort(data,center+1,right) ;

        //并，合起来
        merger(data,left,center,right) ;  
    }
}

merge(data, left, centre, right)
    n1= centre – left + 1
    n2= right - centre

    //建立一个新数组
    let L[ 0..n1] and R[ 0.. n2] be new arrays
    
    //填充数组
    for 𝑖= 0 to n1
        L[ 𝑖] = data[ left + 𝑖]
    for j = 0 ton 2
        R[ 𝑗] = data[ centre + 𝑗]
    
    L[ n1] = R[ n2] = ∞
    𝑖= 𝑗= 0

    //比较与更新数组
    for 𝑘= left toright
        if L[ 𝑖] ≤R[ 𝑗]
            data[ 𝑘] = L[ 𝑖++ ]
        else data[ 𝑘] = R[ j++ ]

实现——完全代码：百度百科

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class MergeSort{
    public static void main(String []args){
        int [] arr = {9,8,7,6,5,4,3,2,1}; //测试数组
        mergeSort(arr);
        System.out.println(Array.toString(arr));
    }


    public static void mergeSort(int []arr){
        int []temp = new int[arr.lengrh] ; //可以在这里的排序前就先建立一个临时数组，避免递归中频繁开辟新空间   

        mergeSort(arr,0,arr.length-1,temp) ; //递归调用一个重载的方法
    }

    public static void mergeSort(int[]arr,int left , int right , int[]temp){
        if(left<right){
            //左还小于右，就说明还没结束
            //等于时就是BaseCase

            mergeSort(arr,left,mid,temp) ; 
            mergeSort(arr,mid+1,right,temp) ; 
            merge(arr,left,mid,right,temp) ; //利用一个方法进行合并
            //而且，需要每次合并完才可进行下一次归
        }
    }

    private static void merge(int[] arr , int left , int mid , int right , int[] temp){
        int i = left ; 
        int j = right ; 
        //小小利用一下双指针进行排序

        int t = 0 ;//结果数组，即之前的临时数组的指针

        while(i<=mid && j<=right){
            //当i j 两边都没排完的时候，我们需要根据二者对应的数值的大小来选择放入临时数组的元素

            if(arr[i] <= j<=right){
                temp[t++] = arr[i++] ; 
            }else{
                temp[t++] = arr[j++] ; 
            }
        }

        //在一边耗完的情况下，把另外一组按顺序排入即可

        while(i<=mid){//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }

        //将结果拷贝至原数组

        while(left <= right){
            arr[left++] = temp[t++];
        }
    }
}

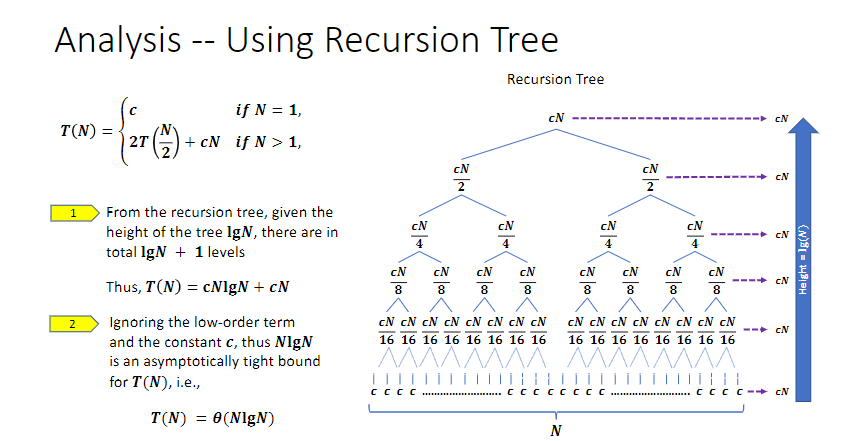
归并排序的算法分析

结论：𝑻(𝑵) = 𝜽(𝑵𝐥𝐠𝑵)

见前文，我们知道了“合并两个已排序的表的时间是线性的” ，舍合并为N
另外，设一次归并排序的完成时间为T(N),其中T(1) = 1
那么，我们知道一次归并排序实际上是：归并排序 = 左侧归并+右侧归并+合并，显然左右的大小可以视作相等，于是可得：
表达式：T(N) = 2*T(N/2)+N ,T(1) = 1
书中的原文表述为：


然后我们可以一直令N = N/2 推公式，并且上下相加削减左右，具体为：

将上述式子逐步相加，于是可以得：

另外，还有一种方式推出公式，于书P197页，这里不再赘述

最后附上MIEC CS211课间中的推导图，和本文的方式是完全一样的：
image.png