树 AVL AVL(Adelson-Velsky and Landis)树是一种自平衡二叉搜索树
简介 搜索树上的大多数原始操作在O(h)时间内在高度为h树上运行,树的高度在一棵AVL树中,是O(lgN)
一棵AVL树是左右子树高度最大相差1的树(其中空树的高度定义为-1)
AVL的平衡,旋转 AVL是特殊化的二叉树,想要保证AVL的平衡,我们可以用到一种称为平衡的做法。是否进行平衡 的问题由树之间的高度决定
AVL的基础定义与高度计算 这里先给出AVL的基本定义以及高度计算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 private static class AvlNode <AnyType>{ AnyType elemenet ; AvlNode<AnyType> left ; AvlNode<AnyType> right ; int height ; AvlNode(AnyType theElement){ this (theElement,null ,null ); } AvlNode(AnyType theElement , AvlNode<AnyType> lt , AvlNode<AnyType> rt){ elemenet = theElement ; left = lt ; right = rt ; } }
高度计算:
1 2 3 4 5 private int theHeight (AvlNode<AnyType> t) { return t == null ? -1 :t.height ; }
旋转 实质上,我们设这里有a这个节点,在插入后只有以下四种情况:
具体理论和原理比较长,见书P86-P91,总之:同向的情况用单旋转,异向的情况用双旋转
单旋转平衡(代码实现) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 private Node rotateWithLeftChild (AvlNode<AnyType> k2) { AvlNode<AnyType> k1 = k2.left ; k2.left = k1.right ; k1.right = k2 ; k2.height = Math.max(height(k2.left), height(k2.right)) + 1 ; k1.height = Math.max(height(k1.left), k2.height) + 1 ; return k1 ; } private AvlNode<AnyType> rotateWithRightChild (AvlNode<AnyType> k2) { AvlNode<AnyType> k1 = k2.right ; k2.right = k1.left ; k1.left = k2 ; k2.height = Math.max(height(k2.left), height(k2.right)) + 1 ; k1.height = Math.max(height(k1.right),k2.height) + 1 ; return k1 ; }
双旋转平衡(代码实现) 1 2 3 4 5 6 7 8 9 10 11 12 private AvlNode<AnyType> doubleWithLeftChild (AvlNode<AnyType> k3) { k3.left = rotateWithRightChild(k3.left) ; return rotateWithLeftChild(k3) ; } private AvlNode<AnyType> doubleWithRightChild (AvlNode<AnyType> k3) { k3.left = rotateWithLeftChild(k3.left) ; return rotateWithRightChild(k3) ; }
AVL的插入和平衡 AVL的核心就在于在插入之后会进行一次对树的平衡 ,具体做法已经在上一部分说过了,这里直接给出对应代码
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 public AvlNode<AnyType> insert (AnyType x , AvlNode<AnyType> t) { if (t == null ){ return new AvlNode <>(x,null ,null ) ; } int compareResult = x.compareTo(t.elemenet) ; if (compareResult < 0 ){ t.left = insert(x,t.left); }else if (compareResult > 0 ){ t.right = insert(x,t.right); }else { } return blance(t) ; } private static final int ALLOWED_IMBAKANCE = 1 ; private AvlNode<AnyType> balance (AvlNode<AnyType> t) { if (t == null ){ return t ; } if (height(t.left) - height(t.right) > ALLOWED_IMBAKANCE){ if (height(t.left.left) >= height(t.left.right)){ t = rotateWithLeftChild(t); }else { t = doubleWithLeftChild(t); } }else { if (height(t.right) - height(t.left) > ALLOWED_IMBAKANCE){ if (height(t.right.right) >= height(t.right.left)){ t = rotateWithRightChild(t) ; }else { t = doubleWithRightChild(t) ; } } } t.height = Math.max(height(t.left) , height(t.right)) + 1 ; return t ; }
AVL的删除 同前文,就是把插入改为删除,或者说“在二叉树原方法的基础上,最后加入平衡的步骤”
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 private AvlNode<AnyType> remove (AnyType x , AvlNode<AnyType> t) { if (t == null ){ return ; } int compareResult = x.compareTo(t.elemenet); if (compareResult < 0 ){ t.left = remove(x,t.left) ; }else if (compareResult > 0 ){ t.right = remove(x,t.right) ; }else if (t.left != null && t.right != null ){ t.elemenet = findMin(t.right).elemenet ; t.right = remove(t.elemenet , t.right); }else { t = (t.left != null ) ? t.left : t.right ; } return balance(t) ; }
小结 1.在AVL树中,对于树中的每个节点,左右子树的高度最多可以相差一个,即高度平衡。平衡是AVL的核心,毕竟是自平衡树
高级树简介 下面写的树多归“高级数据结构”内容了,这里只作简介/应试要求
红黑树 红黑树是 AVL 树的替代品,红黑树也是一种自平衡二叉搜索树一个额外的位来存储节点的颜色 ,可以是红色或黑色
红黑树确保从根到叶的路径不超过任何其他路径的两倍 ,因此树是近似平衡的
基本性质与基本介绍 1.每个节点都是红色或黑色所有简单路径都包含相同数量的黑色节点
插入 插入的基本规则是:根和null节点必须是黑
步骤:从上到下修复颜色
小结 •红黑树是自平衡二叉搜索树
伸展树SplayTrees splay树保证从空树开始的任意M个连续树操作最多花费O(MlgN)时间并不坏 ,只要它发生的频率相对较低 ,就是说不去把重点放在考虑处理最坏情况上,而是优化最坏情况发生的频率
基本性质 1.展开深度为 d 的节点 x 需要 𝜽(𝒅) 时间,即与访问 x 的时间成正比的时间
2.展开不仅将 x 移动到根,而且将访问路径上每个节点的深度大致减半
插入和删除节点需要 𝑶(𝐥𝐠𝑵) 摊销时间
B树 渐近分析假设整个数据结构在计算机的主存中,当数据大小大于主存容量时,部分数据结构必须存储在磁盘上。如果发生这种情况,算法的渐进效率将变得毫无意义,因为磁盘访问比访问存储在内存中的数据慢得多。
B-tree 及其变体,如 B+-trees 和 B*-trees,是为了提高树操作的效率而开发的
基本性质 M 阶 B 树是 M 叉树
请注意,B 树有许多变体,每种变体的属性都略有不同。上述属性适用于 B-tree 的一种流行变体,称为 B+-tree
使用方式 同MIEC原笔记
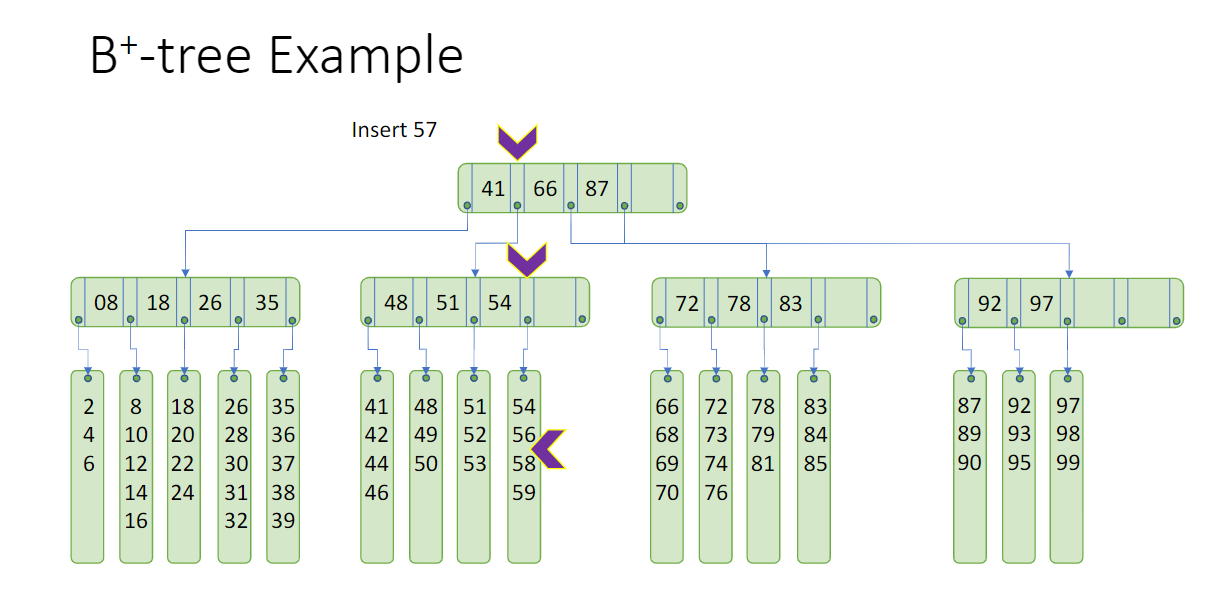 # 这是啥
# 这是啥




