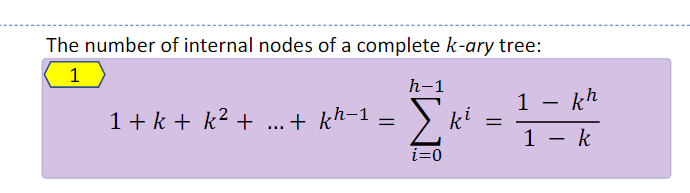1.0 树：树的简介，二叉树的实现

树

树/自由树(tree/free tree)是一个连通的、非循环的无向图

前文

初步阐释了树，以及对于二叉树、AVL树的实现与分析。
最后简单介绍了红黑树、伸展树、B/B+树，如果有需要/有机会的话补充这三者的实现与分析(好复杂)

树的介绍

树有多种方式定义，其中一种自然的方式是采用递归
一棵树是一些点的集合，这个集合也能是空集；
若不为空集，树就由称作跟root的节点r，以及0到N个的非空(子)树组成，子树的每一棵的跟都有来自r的一条有向边连接
在递归定义中，我们认为“一棵树是N个节点和N-1跳边的集合，其中一个节点为根root”

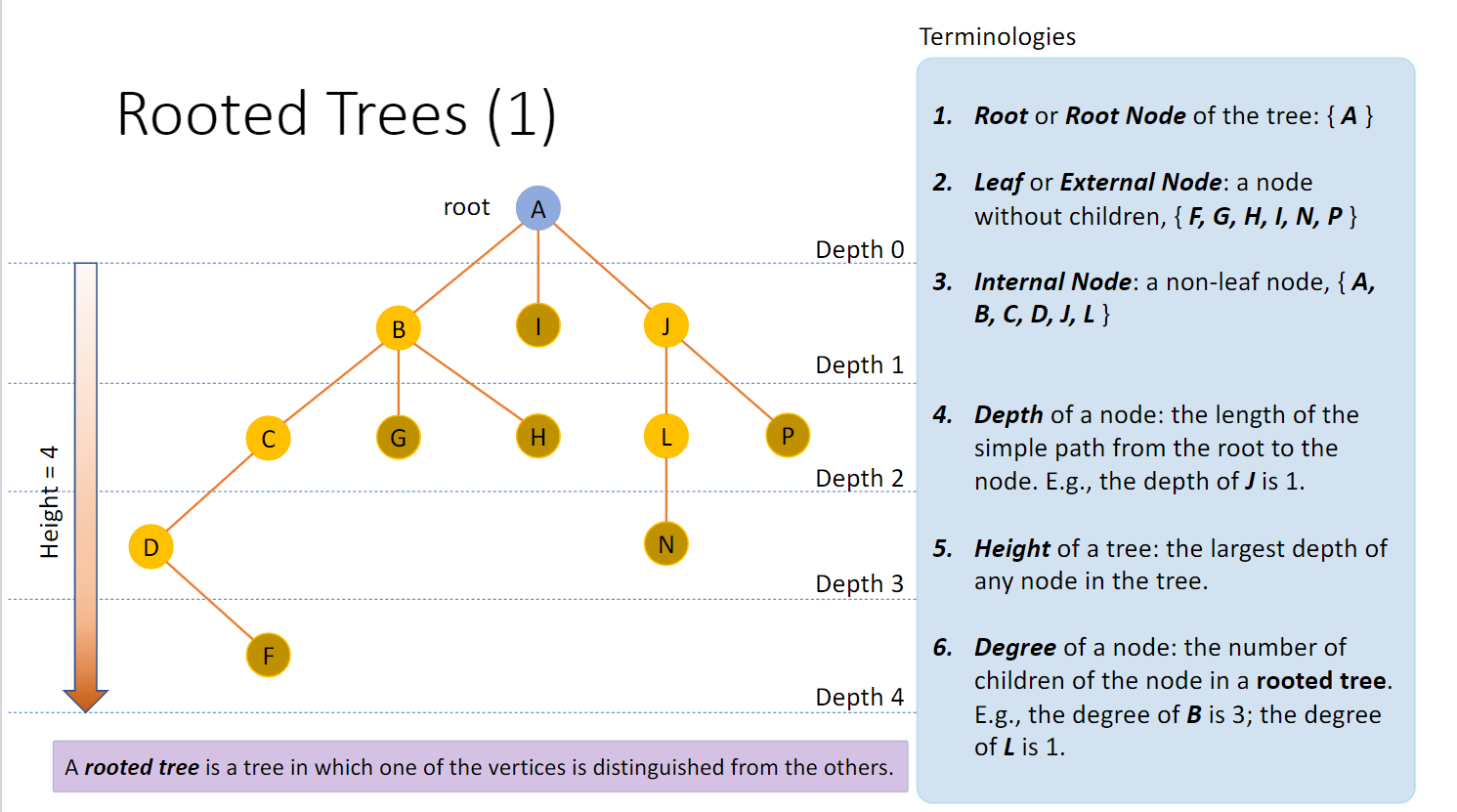
树与节点

根节点：最初的节点，被称为根或根节点 Root/Root Node
叶/外节点:没有子节点的的点 Leaf/External Node
内节点：非叶节点的其他节点 Internal Node

深度Depth:从根到节点的简单路径的长度
高度Height:一棵树的最大深度，对于任意节点ni,ni的深度到一片树叶的最远路径长
Degree 根节点的子节点数目

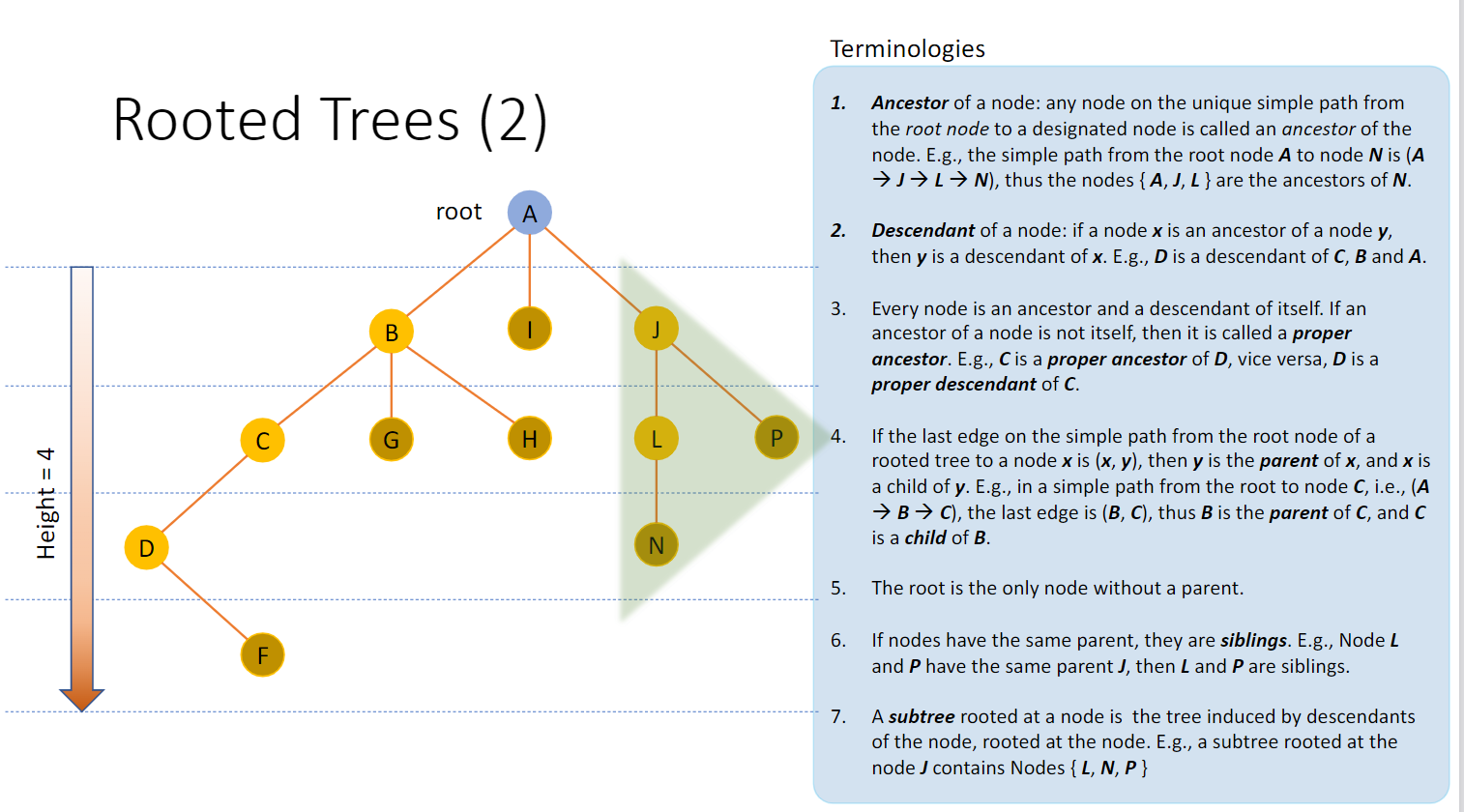
节点祖先 Ancestor of a node：从根节点到指定节点的唯一简单路径上的任何节点
后代 Descendant: 如果A是B的祖先节点，则B是A的后代节点

每个节点都是自己的Ancestor和Descendant

父节点 Parent:从根节点到指定节点的简单路径上的最后一条边的那个点，则是指定节点的父节点。根节点是唯一没有父节点的节点

同级节点 siblings:如果两个节点拥有相同的父节点，则它们是同级节点

子树和子树根节点 :以节点为根的子树是由以节点为根的节点的后代生成的树

树与节点的基本表示

对于树，最重要的是表现出其节点。通过存储根节点，我们就实际上存储了树

class TreeNode{
    Object element ; 
    TreeNode firstChild ; 
    TreeNode nextSibling; 
}

可以用以下代码来表示树和节点(MIEC版，更详细):

public class BinarySearchTree<K extends Comparable<K>, V> {
    private Node root;
    private class Node {
        private K key;
        private V value;
        private Node leftChild, rightChild;
        public Node(K key, V value) {
            this.key = key;
            this.value = value;
        }
    }
    public void insert(K key, V value) { ... }
    public void delete(K key) { ... }
    public void max( ) { ... }
    public void min( ) { ... }
    public void successor(K key) { ... }
    public void predecessor(K key) { ... }
    public void search(K key) { ... }
    public void inOrderWalk( ) { ... }
    ...
}

二叉树 Binary Tree

代码实现部分见“二叉树及相关功能实现”

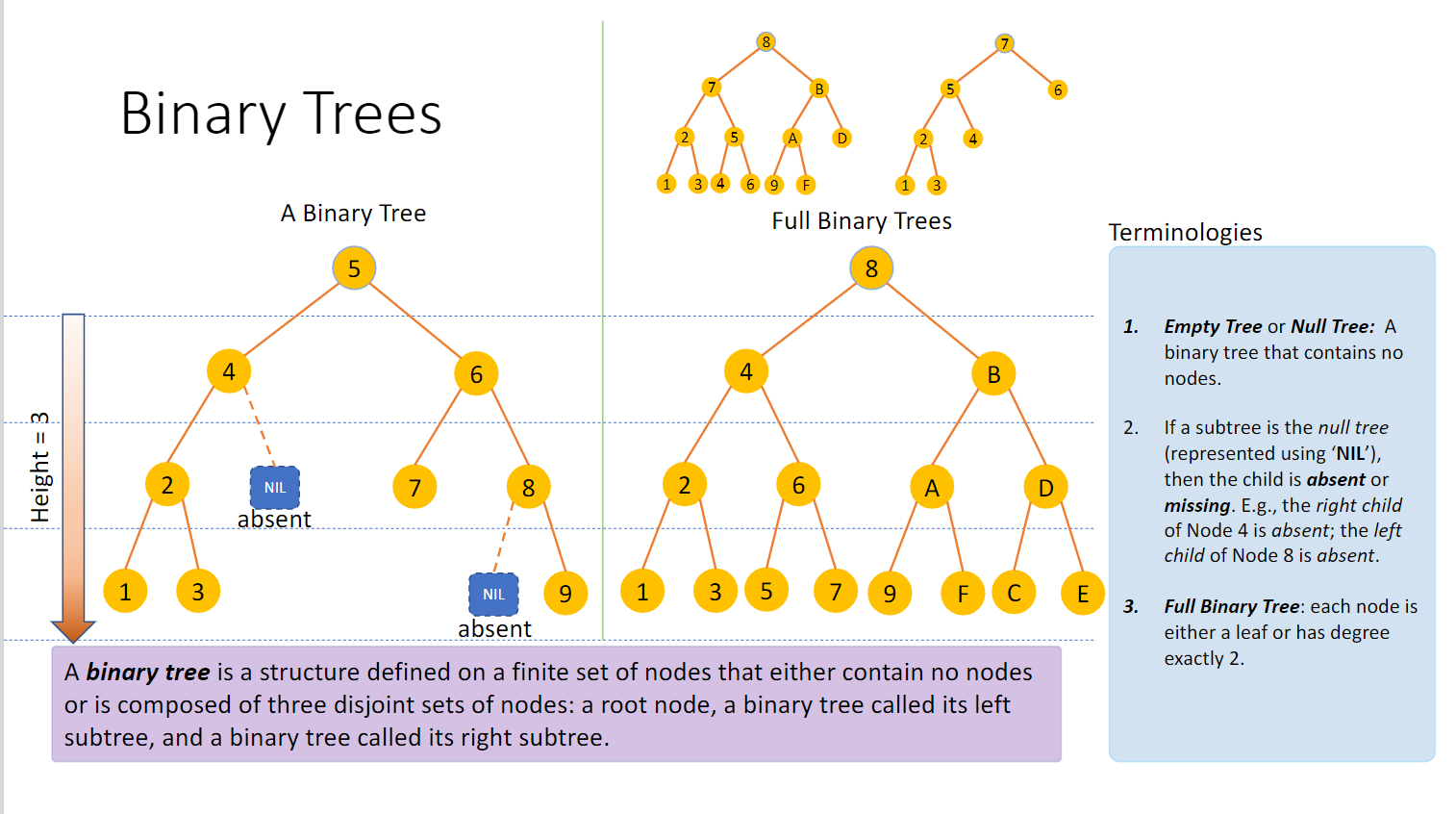
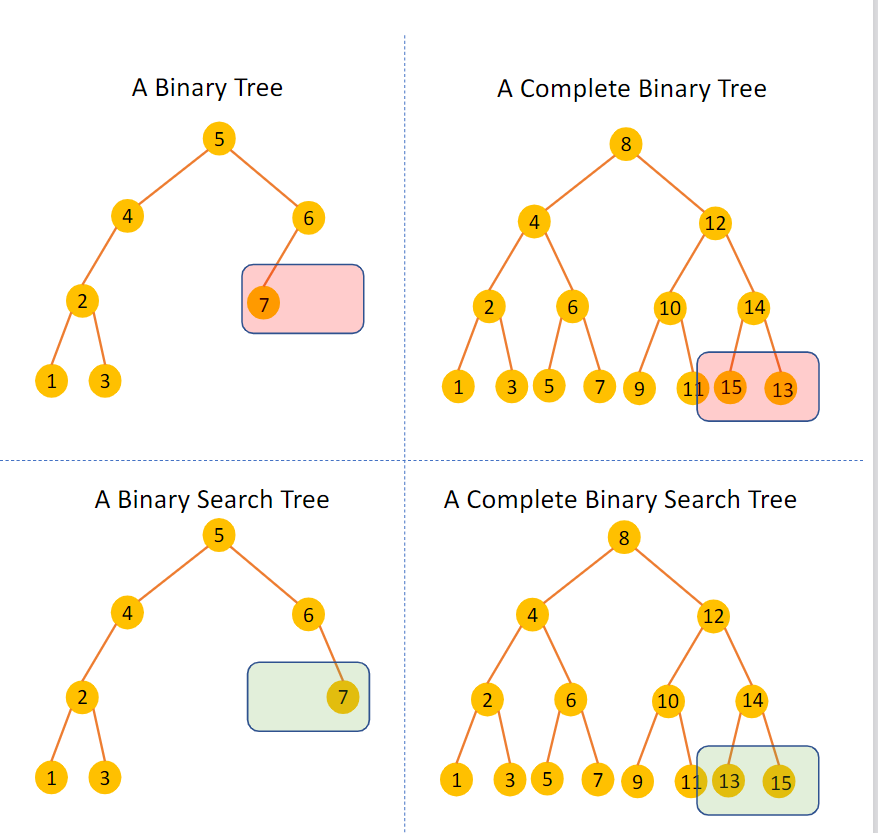
二叉树是在有限的节点集上定义的结构，这些节点集要么不包含节点，要么由三个不相交的节点集组成：根节点、称为左子树的二叉树和称为右子树的二叉树

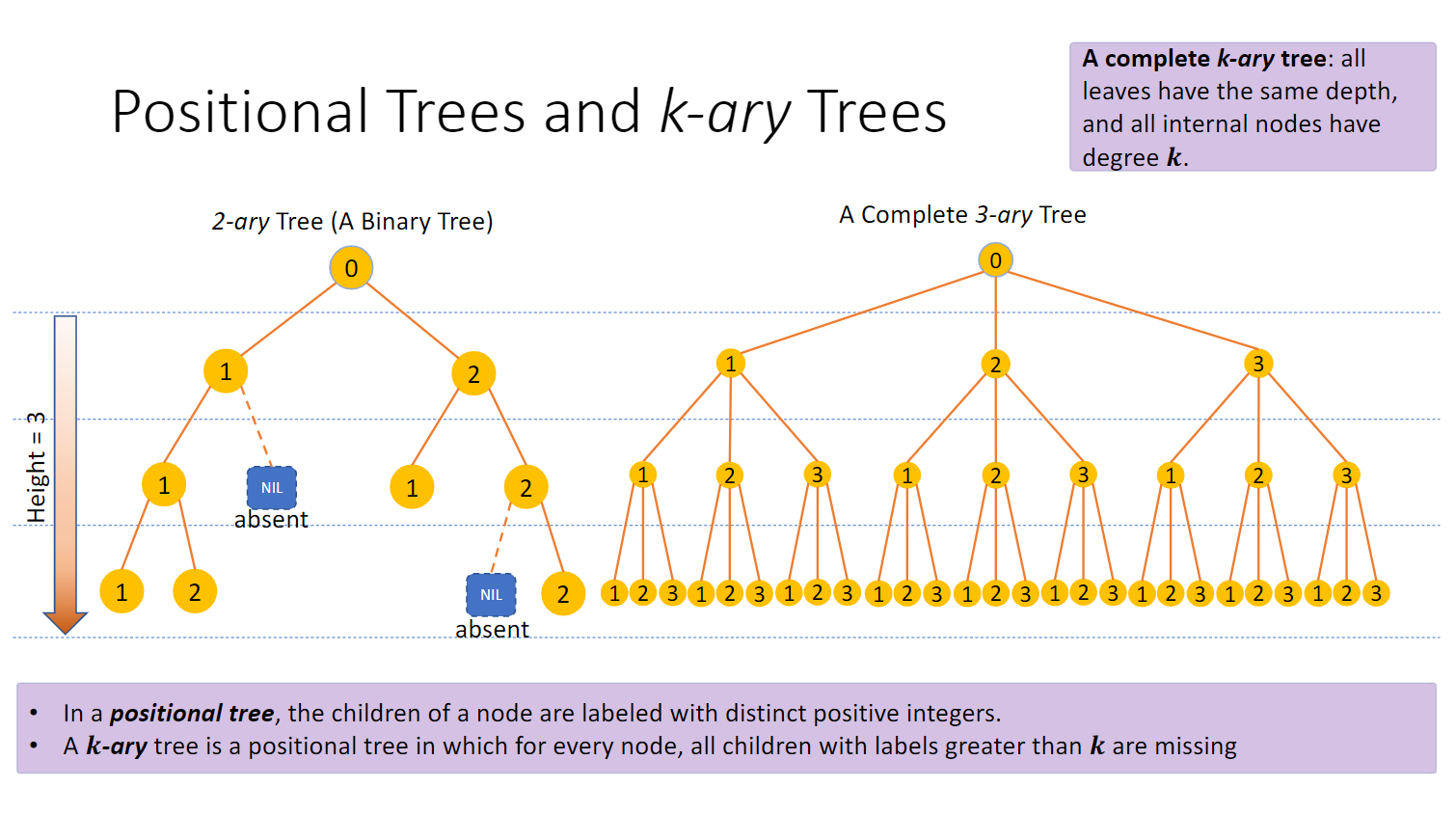
Positional Trees and k-ary Tree

k-ary Tree 中的内节点(即不是叶节点的节点)数量

二叉搜索树 Binary Search tree BST

二叉搜索树（BST）是一种二叉树，其中每个节点都有一个可比较的键（和一个关联值），并满足以下限制：任何节点中的键大于该节点左子树中所有节点中的键，小于该节点右子树中所有节点中的键

或者说，对于某个节点对应的值而言，这个值总是大于其左边的值而小于其右边的值

“A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all nodes in that node’s left subtree and smaller than the keys in all nodes in that node’s right subtree.”

树的遍历(基本介绍)

这里基本提一下树的三种遍历方式，详细的代码实现和介绍，于本文《细说树的遍历》一部分

我们前面说过，我们的树自然是使用递归来生成/操作的，自然，想要遍历一棵树，最先想到的也是利用递归。根据目的和实现，我们最常使用三种遍历：先序遍历、中序遍历、后序遍历

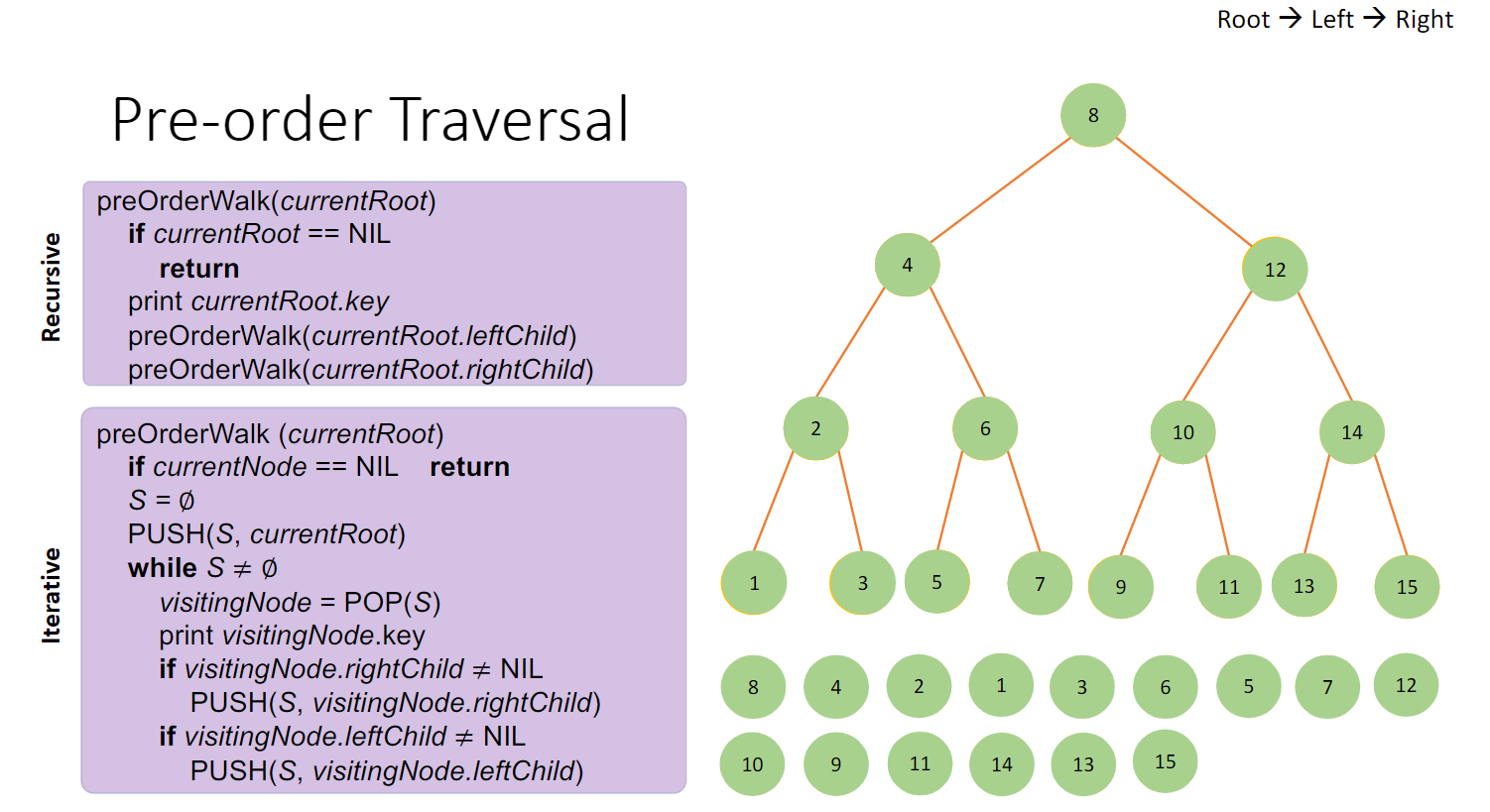
先序遍历：先处理当前节点，再处理两棵子树
中序遍历：依次序列出各项，处理左子树、当前节点、右子树
后序遍历：先处理两棵子树，再处理当前节点

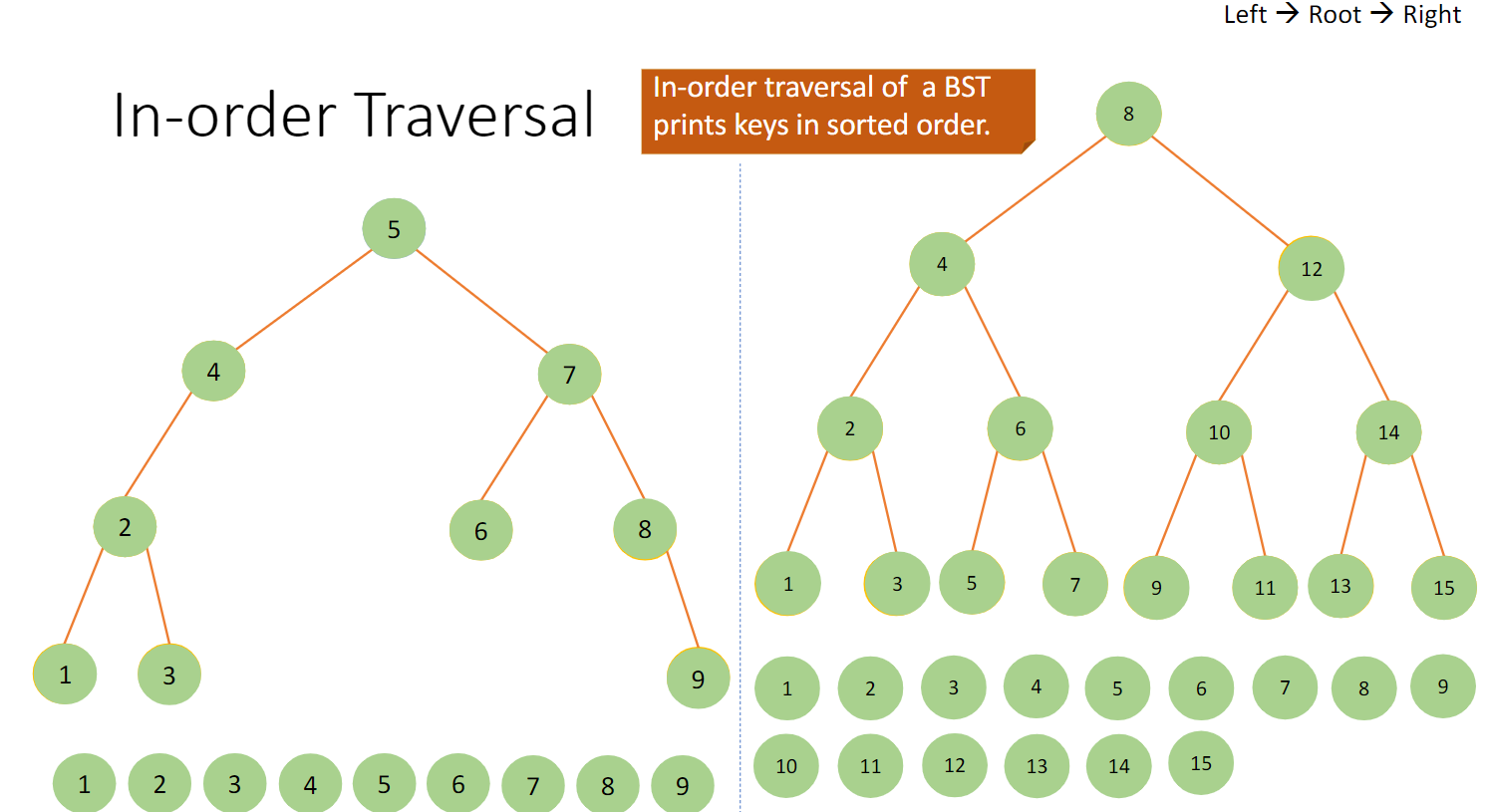
BST:In-Order

按照Left->Root->Right的顺序输出结果

我们可以利用递归来实现这种搜索，核心的伪代码如下:

inOrderWalk(currentRoot){
    if(currentRoot == NIL) {
        return ; 
        //如果到了一个NIL结点，则代表已经搜索到底了
    }else{
        //否则继续执行搜索操作  
        inOrderWalk(currentRoot.leftChild);
        print(currentRoot.key) ;
        inOrderWalk(currentRoot.rightChild);
    }
}

核心部分在于else部分，我们逐步分解:

```print currentRoot.key ;```：在完成一次深度搜索之后，会是前一句```inOrderWalk(currentRoot.leftChild);```的后一句，则可以实现打印，此时打印的结果自然就是刚刚第一个完成搜索得到的点 

```inOrderWalk(currentRoot.rightChild);```:同理。在完成一次左向搜索后，进行右向搜索，然后自然又会进入到一波递归中去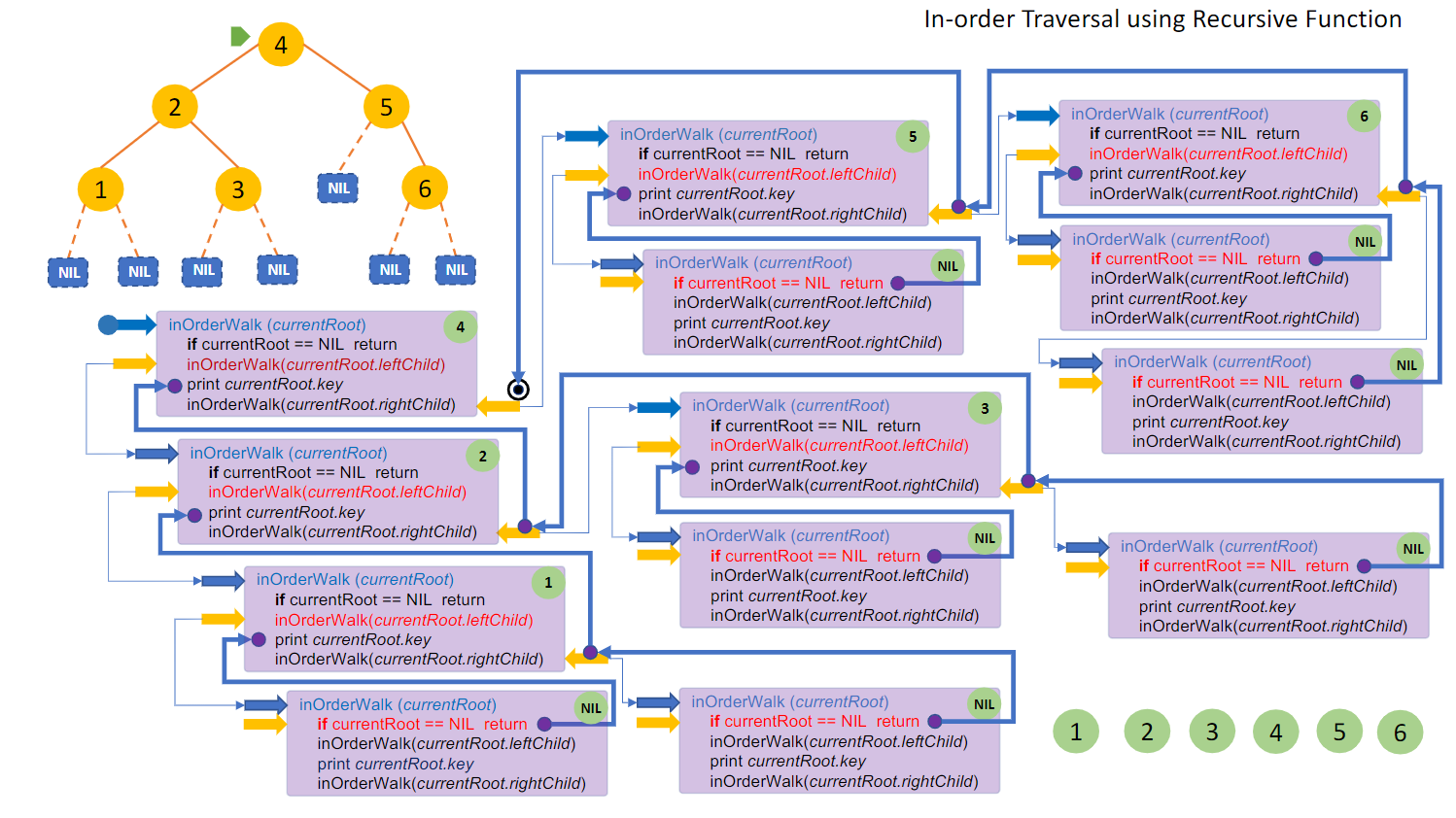 
![](https://s2.loli.net/2022/03/11/mauNDFQ9djhwiqo.png) 

我们同样还可以使用迭代来完成这种搜索，如下：
```Java
inOrderWalk(currentRoot){
    S = ∅
    while S ≠ ∅ or currentRoot ≠ NIL{
        if currentRoot ≠ NIL{
            //如果还没找到NIL，就是还未触底，就一直向左找并压入栈
            PUSH(S, currentRoot)
            currentRoot = currentRoot.leftChild
        }else{
            //触底后进行一次弹出，并且打印，然后开始向右搜索
            currentRoot = POP(S)
            print currentRoot.key
            currentRoot = currentRoot.rightChild
        }
    }
}

可以想象：在首次压栈的过程中，我们不断加入了最左边的一排结点，触底后，我们开始出栈并打印值，此时实际上是从下到上再次进行了一次搜索，不过这次的目的是打印值与向右搜索。如此反复，则可以得到结果。
核心原理和递归的做法是一样的

BST：Pre-order

同样有两种搜索法,思想和做法同上，只是打印顺序不同:

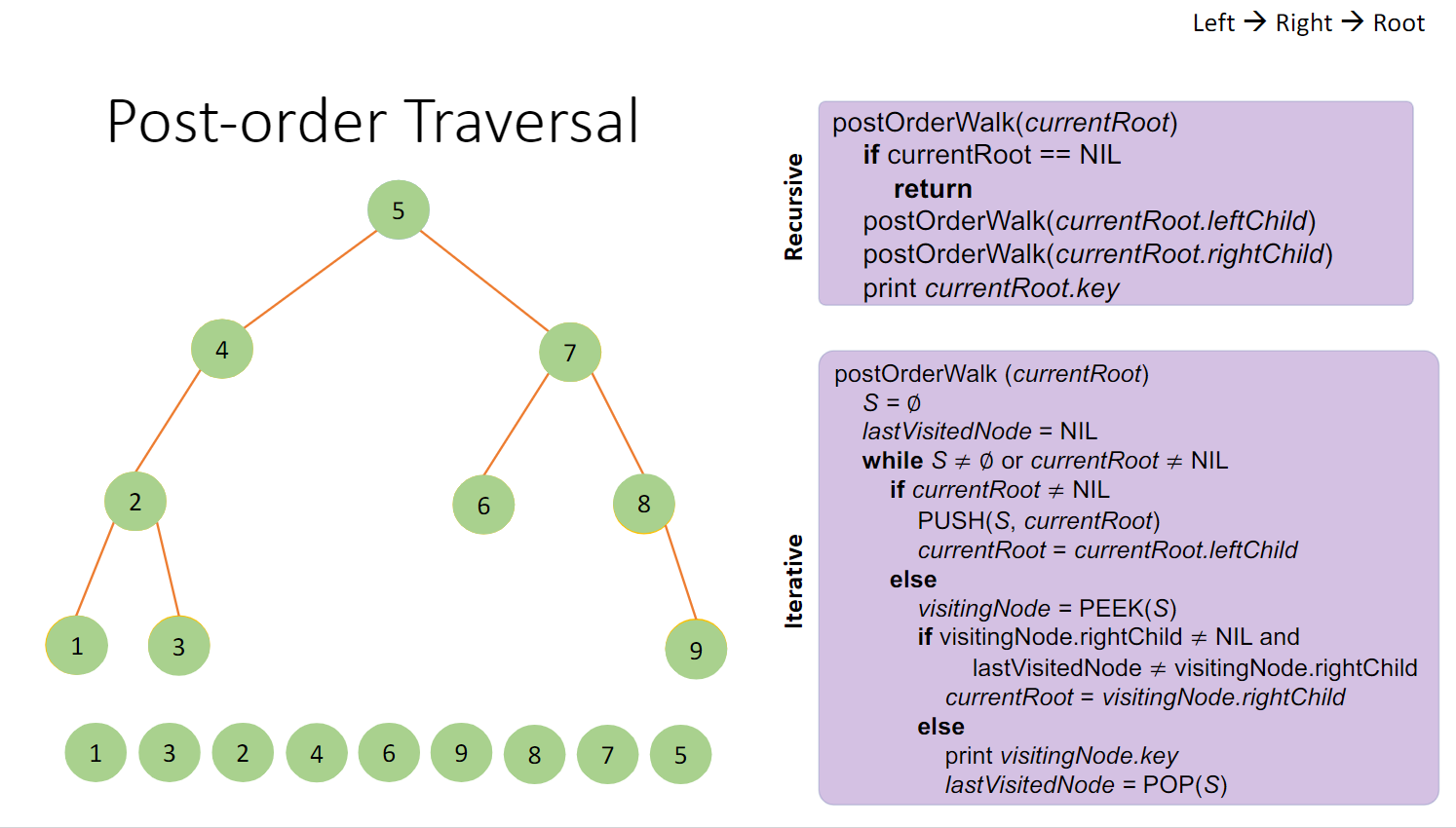
BST:Post-order

同样有两种搜索法,思想和做法同上，只是打印顺序不同:

小结

对于上述的三种搜索法，我们可以归纳为:
递归:

Methond(当前节点){
    若为空返回  

    若不为空，则{
        A.打印当前
        B.左搜索
        C.右搜索

        上述ABC按要求排序，如对于in-Order，则是BAC(左，当前，右)
        对于pre-order则是 ABC(当前，左，右)
    }
}

迭代：
迭代都是利用栈进行，因此和递归法大同小异:

Methon(当前节点){
    如果不为空{
        压入
        按需搜索
    }

    如果为空{
        出栈
        打印
        按需搜索
    }
}

在这里和递归相比，各模式的实现的差别较大，建议分别阅读

Level-order Traversal

如果依照层次(即深度)来完成搜索，则要利用到队列

Level-order按水平顺序，从上到下打印

levelOrderWalk (currentRoot){
    Q = ∅
    ENQUEUE(Q, currentRoot)
    //首先另队列为空，然后让该节点入队
    while Q ≠ ∅{
        //如果队列不是空的，按下执行操作
        currentNode = DEQUEUE(Q)    
        print currentNode.key   
        //首先让当前节点出队，并打印

        //然后按照左右节点的情况分别让对应的节点入队
        //这里我们按照先左后右的顺序，以此达到了水平顺序遍历的目的  
        if currentNode.leftChild ≠ NIL 
            ENQUEUE(Q, currentNode.leftChild )
        if currentNode.rightChild ≠ NIL 
            ENQUEUE(Q, currentNode.rightChild )
    }

}

二叉树及相关功能实现（源于书本）

基础与节点定义

同最基本的树的节点，但我们根据二叉树的性质定义了专门的变量

class BinaryNode{
    Object element ; 
    BinaryNode left ; //左子树
    BinaryNode right ; //右子树
}

利用泛型，做出更普遍性的定义:

private static class BinaryNode{
    AnyType element ; 
    BinaryNode<AnyType> left ; 
    BinaryNode<AnyType> right ; 

    //构造
    BinaryNode(AnyType theElement){
        this(theElement,null,null);
    }

    BinaryNode(AnyType theElement ,BinaryNode<AnyType> lt , BinaryNode<AnyType> rt ){
        element = theElement ; 
        left = lt ; 
        right = rt ; 
    }
}

后续都会以泛型版本的来写方法，主要使用compareTo方法，而且开销也会来源于此。这些是后话了

二叉树的基本方法

插入方法insert

private BinaryNode<AnyType> insert (AnyType x , BinaryNode<AnyType> t){
    if(t == null)
        return new BinaryNode<>(x , null , null);

    int compareResult = x.compareTo(t.element)
        //依据对比结果进行插入

    if(compareResult < 0){
        //小于，尝试往左边插值
        t.left = insert(x,t.left);
    }else if(compareResult > 0 ){
        t.right = insert(x,t.right);
    }else{
        //这里不讨论相等的情况，重复元素处理/更新之后再说
        //找到相同的，一般有两种策略，“更新”，或者“同时存储二者”    
    }

    return t ; 
}

是否有某个值:contains

/*
    X是我们要查找的item， t是传入搜索的node，一般最开始的root，后面是递归时的对应点
    若找到了才返回true,否则返回false    
*/

private boolean contains(AnyType x , BinaryNode<AnyType> t ) {
    if(t == null){
        return false; 
        //如果寻找的点空掉了，那肯定就没有了
        //而且，也是一个baseCase
    }

    int compareResult = x.compareTo(t.element) ; 
    //调用compareTo方法来进行比较

    if(compareResult < 0 ){
        return contains(x,t.left) ; 
        //小于0代表着x的数值小于参数（即t.item）,那么我们向左递归继续找
    }else if(compareResult > 0 ){
        //大于0同理
        return contains(x,t.right) ; 
    }else{
        //=0,相等
        return true ;
    }
}

最值查找findMin/findMax

其二，我们需要知道如何得到最值，事实上这些内容都大同小异：
包含两种方法递归和非递归实现,以左树为递归例子，右树为非递归例子
在树中的查找，实际上是不比较值的，找小的就一直往左到底部，找大的同理
因为值的比较，实际上是在生成树的时候就进行的了

//%递归查找(Min)
private BinaryNode<AnyType> findMin(BinaryNode<AnyType>){
    if(t == null){
        return null ;
    }else if(t.left == null){
        //没有更左边的点了，那这一个点显然就是我们找到的最小值
        return t ; 
    }

    return t.findMin(t.left) ; //如果没有发生上文的情况，就意味着我们要继续向左搜索
}


//%非递归查找(Max)
private BinaryNode<AnyType> findMax(BinaryNode<AnyType>){
    if(t != null){
        while(t.right != null){
            t = t.right ;
            //t不为空，t的右侧不为空，那么显然就更新t，然后继续右行
        }

        return t ; 
    }
}

二叉查找树的基础实现

删除方法remove

删除反而是普通二叉树中最麻烦的事情，因此单独拿出来说
一般认为有惰性删除与完全删除
惰性删除：把要去除的元素标记为，但是实质并没有把它从树中移除，这种方法除了偷懒之外还有益处，具体为：

二是完全删除，这个方法就是改变了节点之间的连接方式，彻底将元素移出树
理论操作如下，节选自书：


其代码实现如下：

//返回值是子树的新根,x是我们要删除的部分
//实际上包括两个部分，一个是找x,一个是删除x并更新
private BinaryNodes<AnyType> remove(AnyType x,BinaryNode<AnyType> t){
    if(t != null){
        return t ; 
        //没有这个值就啥都不做
    }

    int compareResult = x.compareTo(t.element) ;
    if(compareResult < 0 ){
        t.left = remove(x,t.left);
    }else if(compareResult > 0 ){
        t.right = remove(x,t.right);
        
        //% 上述的两个情况，实际上是在递归中查找我们要删掉的那个值
        //% 当我们找到了这个值，递归才会进入下面的情况
        //% 在下面的情况中，分为删除节点有两个节点、没有节点、有一个节点的情况

    }else if(t.left != null && t.right !=null){
        //% 此时我们已经找到了那个要删掉的节点了
        //两个子树的情况
        t.element = findMin(t.right).element ; //% 寻找右子树的最小值，让它替代被删除的节点（值代替）  
        t.right = remove(t.element,t.right) ; //% 断开t该位置和原本位置的链接即可
        //@ 这部分内容可能比较抽象，可以结合p83的图4-24理解
        
    }else{
        //剩下的情况就简单了，这个其实才是实质上每次递归最后到达的地方
        t = (t.left != null) ? t.left:t.right ; 
        //若左树不为空，则让该位置变为左树根节点
        //实际就是以“让左树根节点代替删除节点”的方法，一次性完成了删除和更新
        //右树同理。如果没有左树我们就选右树了
    }

    return t  ;
}

平均情况的算法分析

这部分暂略，表达式的求解在快速排序部分有提及。这里引用书本内容：

二叉树及相关功能实现（源于MIEC）

源于课件伪代码进行的实现，建议看源于书本的部分，更详细且更易懂

最值

在二叉树中，按照其规则，最小值位于最左侧，而最大值位于最右侧，这使得我们可以之间向左/向右 搜索来得到最值

findMin(currentRoot)
    while currentRoot.left ≠ NIL
        currentRoot = currentRoot.leftChild
    return currentRoot

findMax(currentRoot)
    while currentRoot.rightChild ≠ NIL
        currentRoot = currentRoot.rightChild
    return currentRoot

插入

Insert(currentRoot,node){
    //接受根以及一个节点作为参数
    if currentRoot == NIL {
        return node ;
        //如果根节点为空，理所当然，我们返回node
        //实质上的意思就是把它作为根节点    

    }

    //下面是根节点非空的情况，我们按照大小顺序来进行位置的插入

    if node.key < currentRoot.key{
        currentRoot.leftChild = insert(currentRoot.leftChild, node);
        //如果node的值比根小，就以根的左值为子树的根，再次向下搜索
        //这里实际上是用了递归  

    else if(node.key < currentRoot.key){
        //同理，大于则向右  
        currentRoot.rightChild = insert(currentRoot.leftChild,node);
        }

    else{
        currentRoot.value = node.value ;
    }
    }


    return currentRoot ; 
}

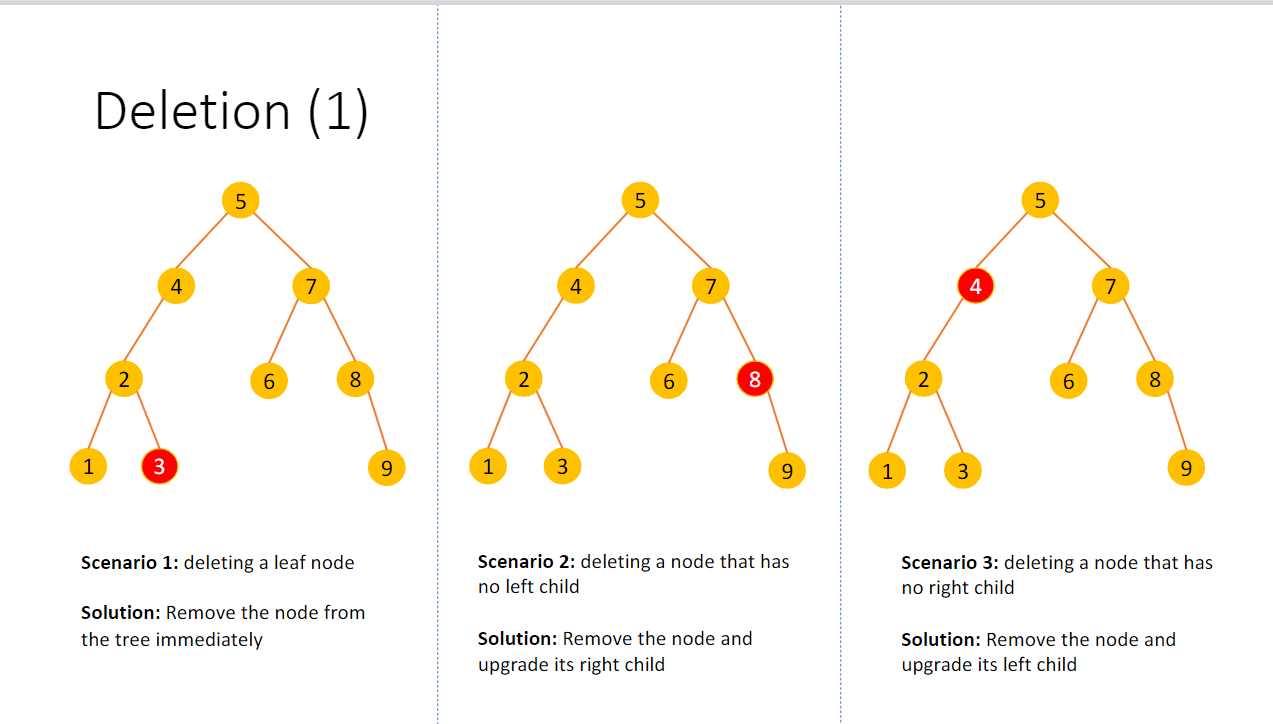
删除

首先我们可以分析三种最基础的情况

分别是对应：本来就是叶节点，没有左/右 子树的情况
对应的解法分别是：直接移除该节点，以及移除该节点后将其右/左子树更新到它之前的位置

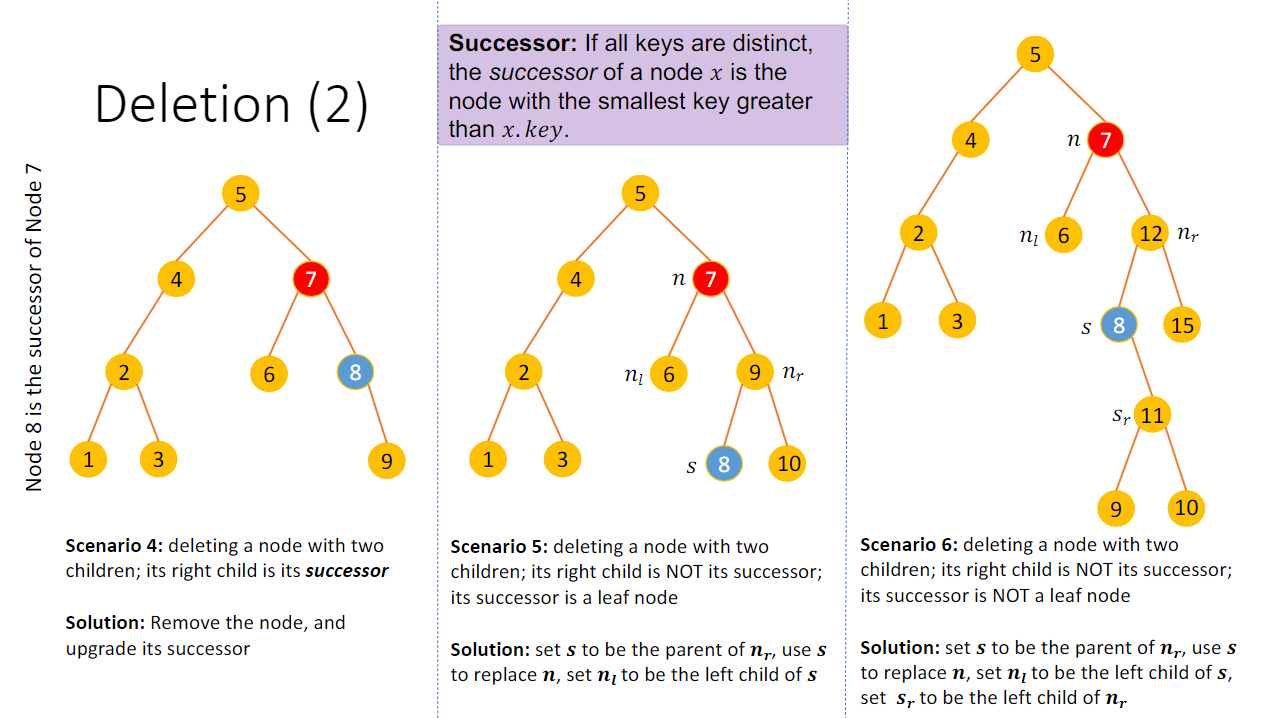
而当要删除的节点的子树情况比较复杂的时候，我们就需要分别考虑并且更新子节点状态

那么，怎么挑选继承被删除位置node x的点？则继承的点应该是子树中最小的点，同时也应该是大于x.key的点

依上分析，我们的代码如下:
我们利用递归来解决该问题：因为实际上，base case和每一步的操作是比较明了的

public static void delete(currentRoot,key){
    if(currentRoot == NIL){
        return currentRoot ; 
        //BaseCase:当输入的结果为空时，则返回该节点
    }

    //下移到要删除的点
    if(key < currentRoot){
        currentRoot.leftChild = delete(currentRoot.leftChild,key) ; 
    }else if(key > currentRoot){
        currentRoot.rightChild = delete(currentRoot.rightChild,key) ; 
    }else if(currentRoot.leftChild != NIL && currentRoot.rightChild != NIL){
        currentRoot.key = findMin(currentRoot.rightChild).key ; 
        currentRoot.rightChild = delete(currentRoot.rightChild , currentRoot.key) ; 
    }else{
        current = (currentRoot.leftChild != null) ? currentRoot.leftChild : currentRoot.rightChild ; 
    }

    return currentRoot ; 
}