cs335计算理论(三)
写在前面
真的痛苦
而且这部分内容对于大二的学生过于晦涩难懂了,而大三大四乃至研究生学生也不至于看这篇博客
所以这一篇文章更适合那些
同在MIEC受苦,且本质快速阅览的学生
如果要一步一步学,建议去观看油管或者B站计算理论的相关视频
正文
Lecture6-7 可归纳性 Reducibility
The Reducibility Method
如果我们知道某个问题(比如 TM)是不可判定的,我们可以用它来证明其他问题是不可判定的
If we know that some problem (say TM) is undecidable, we can use that to show other problems are undecidable
被称为可归约性的方法,可以被用来证明“某个问题在计算上是不可解的”这一问题
归约旨在将一个问题转换为另外一个问题,并且使得可以用第二个问题解决第一个问题
停机问题
$A_TM$是不可判定的,即确定一个图灵机是否接受一个给定的输入问题是不可判定的。
下面我们考虑一个与之相关的问题:$HALT_TM$,即确定一个图灵机对给定的输入是否停机(通过接受或拒绝)
我们把这个问题叫做停机问题 halting problem
若将$A_TM$归约到$HALT_TM$,就可以利用$A_TM$的不可判定性来证明停机问题的不可判定性
Def:
$𝐻𝐴𝐿𝑇_TM$ ={<𝑀,𝑤> | 𝑀 halts on input 𝑤}
$𝐻𝐴𝐿𝑇_TM$ 通过矛盾的反证,可以证明其是不可判定的undecidable
证明了&A_TM&对于$𝐻𝐴𝐿𝑇_TM$是具有可归纳性的
令 TM R 判定decide $𝐻𝐴𝐿𝑇_TM$
构建 TM S 判定 deciding $A_TM$
S = “On input <M,w>
1.使用R来测试M是否在w halts,如果不是,则直接拒绝
2.继续模拟,直到其停止(如R所保证的)
3.如果M已接受则接受;如果M拒绝则拒绝
TM S决定了&A_TM$,由此产生了一个矛盾。因此,$𝐻𝐴𝐿𝑇_TM$是不可判定的
如果R判定$HALT_TM$,则S判定$A_TM$,因为$A_TM$是不可判定的,故$HALT_TM$也必定是不可判定的
可归纳性方法 Reducibility–Concept
如果我们有两种语言(或问题)A和B,A对B是可归纳性的,意味着我们可以用B解决A
Eg1:测量矩形的面积可以简化为测量其边的长度
Eg2:我们证明NFA对于DFA是可归纳的
If A is reducible to B then solving B gives a solution to A
$E_TM$是不可判定的
$E_TM$ is undecidable
$𝐸_TM$ = {𝑀 | 𝑀 is a TM and 𝐿(M) = ∅}
(例题详见书)
赖斯定理 Rice’s themorem
测定语言的任何一个性质是否可由图灵机识别都是不可判定的
另外,检查两个图灵机的等价性是一个不可判定的问题(这条不是赖斯)
归约可映射性 Mapping Reducibility
Def:
对于函数 𝑓:Σ∗→Σ∗ , 如果它是可计算的computable ,如果这里有一个TM F
F可以对于所有的字符串w,使得 on input w 停止 f(w)的磁带上的输出
if there is a TM 𝐹 where 𝐹 on input 𝑤 halts with 𝑓(𝑤)on its tape, for all strings 𝑤.
对于函数 𝑓:Σ∗→Σ∗ 是一个可计算函数,如果有某个图灵机M,使得在每个输入w上M停机,且此时f(w)出现在带子上
Def:
“用映射可归约性将问题A归约为问题B”指的是,存在一个可计算函数,它可以将问题A的实例转化为问题B的实例。
如果有这么一个转化函数(我们称它为归约),就能用B的解决方案来解A
形式化定义
语言A是映射可归约性到语言B的,如果存在可计算函数𝑓:Σ∗→Σ∗,使得对于每个w,w∈A <=> f(w)∈B
记作 A<=$_m$B。称函数f为从A到B的归纳
Mapping Reducibility 性质
Thm:若A<=mB ,若B是可判定的,那么A也是可判定的
推论:若A<=mB,如果A是不可判定的,那么B也是不可判定的
Thm:若A<=mB,且B是图灵可识别的 ,则A也是图灵可识别的
推论:若A<=mB,且A不是图灵可识别的,则B也不是是图灵可识别的
图灵可识别的 T-recognizable
值得注意的差异:
𝐴 is reducible to 𝐴 𝐴 may not be mapping reducible to 𝐴
for example $A_TM$` !<= m$A_TM$
模板
若想要证明B是不可判定的:
证明一个不可判定的A,它对B是可归纳的
假设TM R 判定B
构建TM S,S判定A,然后证明矛盾
若想要证明 B 是 T-unrecognizable
证明一个 T-unrecognizable A 对于B是映射可归纳性的
给出一个可归纳函数f
(例题详见书)
为了证明某种语言B是不可判定的,证明$A_TM$(或任何已知的不可判定语言)对于B是可归纳的即可
To prove some language B is undecidable, show that $A_TM$(or any known undecidable language) is reducible to B.
TM Configurations
Def:
A configuration of a TM is a triple
q = 状态 the state
p = 头部的位置 the head position
t = 磁带的内容 tape contents
M的格局就像计算中间的一个快照。格局由控制状态,读写头位置,带子内容组成
TM Computation Histories
Def:
An (accepting) computation history for TM M on input w is a sequence of configurations C1,C2,…,C_accept that M enters until it accepts
在输入上的TM(接受)计算历史记录是一系列配置C1,C2,…,C接受,直到它接受
设M是一个图灵机,w是一个输入串。M在w上的一个接受计算历史是一个格局序列C1,C2,…,CL,其中C1是M在w上的一个起始格局,C1是M在w上的起始格局
Cl是M的一个接受语言,且每个Ci都是Ci-1的合法结果,即符合M的规则
M是w上的一个拒绝接受历史。可类似的定义,只是Ci是一个拒绝格局
计算历史方法是证明$A_TM$可归约到某些语言的重要技术。在证明某个问题的不可判定性时,如果这个问题涉及检查某样东西的存在性
计算历史方法就会很有用
计算历史都是有限序列。如果M在w上不停机,则M在w上既没有接受也没有拒绝计算历史的存在。
确定型机器在任何给定的输入上最多只有一个计算历史。
非确定机器即使在单个输入也有可能有多个计算历史,它们与各个计算分支相对应
线性有界自动机 Linearly Bounded Automata
Def:
A linearly bounded automaton (LBA) is a 1-tape TM that cannot move its head off the input portion of the tape.
线性有界自动机(LBA)是一种单磁带TM,不能将其磁头移出磁带的输入部分。
线性界限自动机不允许其读写头离开包含输入的带子区域,是只有有限存储的图灵机。
它只能解决“所需要的存储不得超过用作输入的带子区域”的问题
每个CFL都可由一个LBA来判定
设M是有q个状态和g的个带子符号的LBA。则对于长度为n的带子,M恰好有$qng^n$个不同的格局
这个定理会帮助我们判定M的状态:如果M不是接受也不是拒绝,而在M上模拟$qng^n$步后如果还没有停机,它肯定陷入了循环
对于LBA,接受问题是可判定的。但是对图灵机则不是。
recap:Computation History Method
Computation History Method,有助于证明涉及测试某个对象是否存在的问题的不可判定性
Computation History Method is useful for showing the undecidability of problems involving testing for the existence of some object
D:(多项式方程)有积分解吗?
$E_LBA$:是否是否有一些可接受的字符串(用于LBA)?
PCP:是否有匹配(针对给定的多米诺骨牌)?
$ALL_CFG$:是否有一些被拒绝的字符串(用于CFG)?
在每种情况下,对象都是某种形式的Computation History
Lecture 08 时间复杂度
TIME
介绍
在一个1-tape图灵机M中,M可以decide A.对应输入长度为n的磁带,M最多会使用$cn^2$次,这里的c是某些确定的常数c
模型依赖 Model Dependence
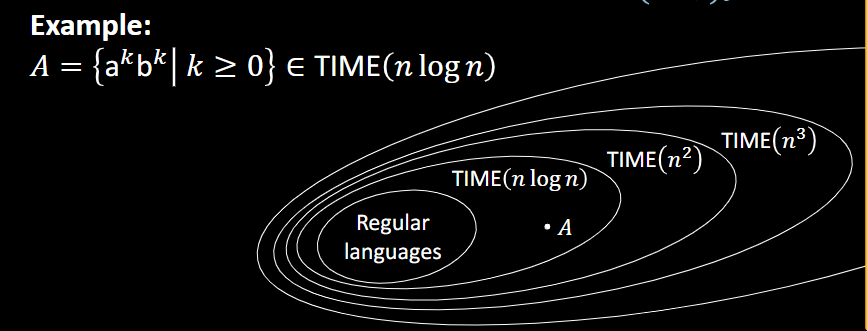
对于同一个A = {$a^k b^k$ | k>=0} 而言,我们可以知道以下事情:
1.
1-tape TM 为 O(nlogn)
Multi-tape TM 为 O(n)
2.二者在不同理论方面的重要程度不同
对于可计算理论,两种模型的选择并不重要
对于复杂性理论,它依赖模型,但是对于合理的确定型模型。我们将更关注那些不依赖于模型选择的问题
所以之后的笔记中,我们将继续使用1-tape TM 来作为复杂性理论的研究模型
时间复杂类
设 𝑡: ℕ→ℕ. 我们认为 TM M 可以在t(n)内执行 runs in time t(n) 如果可以满足:
对于所有的输出长度为n的,M总是在t(n)次步骤中完成
TIME 𝑡 𝑛 ={𝐵|some deterministic 1-tape TM 𝑀 decides 𝐵 and 𝑀 runs in time 𝑂(t(n))}
Multi-tape 与 1-tape
设t(n)>=n,如果 multi-tape TM 在时间t(n)内决定B,则我们可以认为
𝐵 ∈ TIME($t^2$(n))
因为我们想要让1-tape TM 来模拟 Multi-tape 中的一步,就需要O(t(n))步来实现
对于其它合理的确定型模型,我们可以得到类似的结果
模型间的关系
两个计算模型如果可以通过多项式开销 polynomial overhead 来模拟另外一个模型,那么它们之间就是多项式相关的
它们之间的复杂度的关系是 $t$(n) 和 $t^k$(n)
所有的合理的确定型模型都是多项式相关的,比如
1-tape TMs
multi-tape TMs
multi-dimensional TMs
random access machine(RAM)
celluar automata
P类
定义
P = $U_k$TIME($n^k$)
= 多项式时间可判定语言 polynomial time decidable languages
显示多项式时间:每个阶段应明确多项式和总步数多项式
To show polynomial time: Each stage should be clearly polynomial and the total number of steps polynomial
PATH and HAMPATH
𝑃𝐴𝑇𝐻 = {(𝐺,𝑠,𝑡) | 𝐺 is a directed graph with a path from 𝑠 to 𝑡}
PATH ∈ P
HAMPATH = {(G,s,t) | G is a directed with a path rfrom s to t and the path goes through every node of G}
(这条路径就叫做 Hamiltonian path)
由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次
HAMPATH 的时间是指数时间而不是多项式时间
Lecture9 NP 类
不确定性复杂性 Nondeterministic Complexity
在一个非确定性TM (NTM) 决策器中,所有分支对于所有输入都是可停止的
DEFN:
1.一个NTM,如果对于所有输入长度为n的输入,它的所有分支都可以在t(n)步骤下停止。那么我们则称”An NTM runs in time t(n)”
2.NTIME(t(n)) = { 𝐵 |some 1-tape NTM decides 𝐵 and runs in time O(t(n))}
3.NP = $U_k$NTIME($n^k$)
= nondeterministic polynomial time decidable languages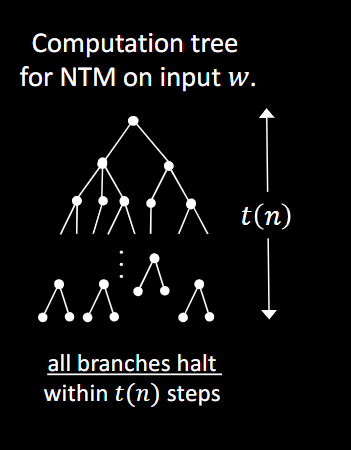
HAMPATH
HAMPATH ∈ NP
(HAMPATH的定义见Lecture 08)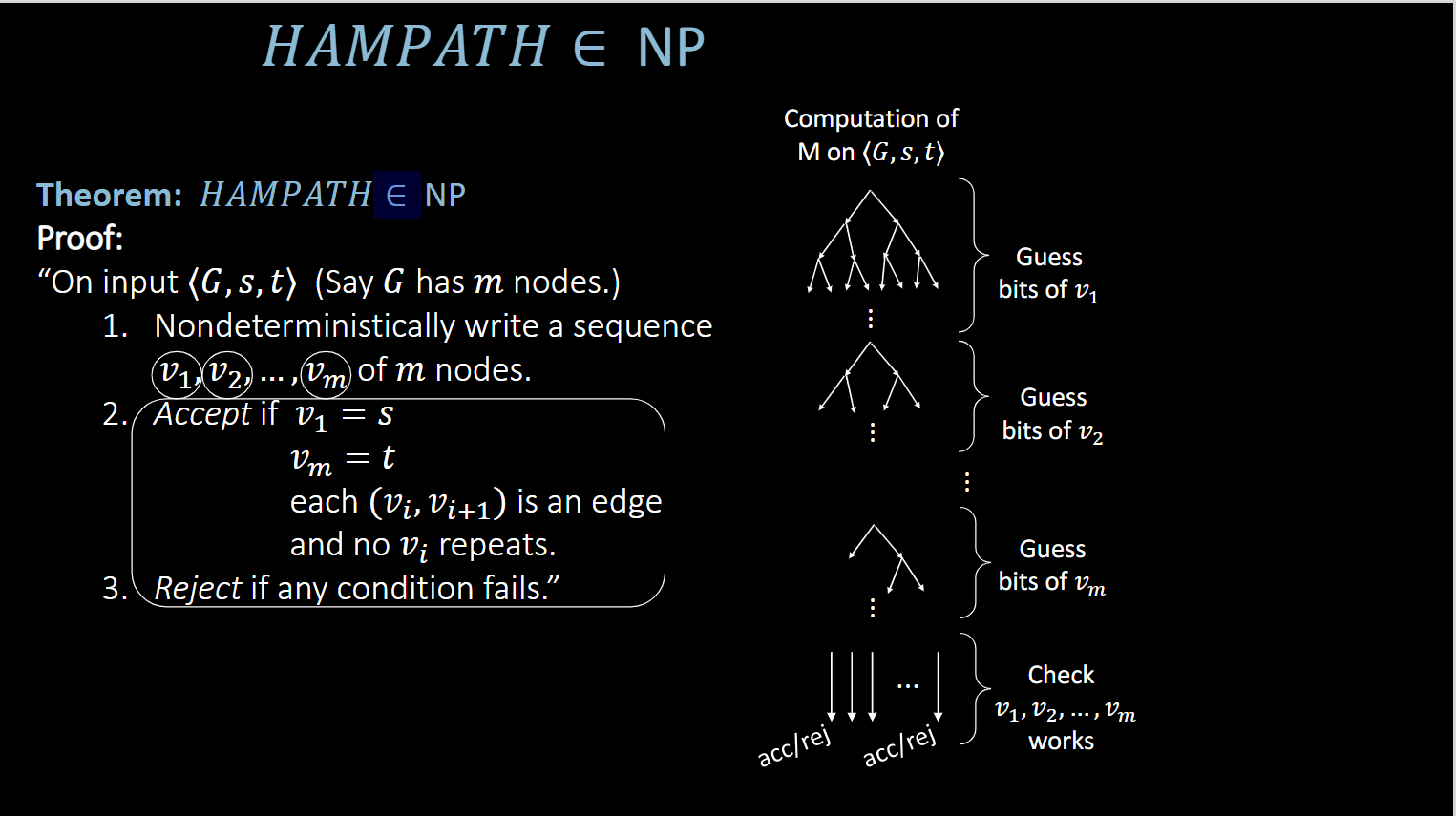
COMPOSITES
定义
𝐶𝑂𝑀𝑃𝑂𝑆𝐼𝑇𝐸𝑆 ={𝑥|𝑥 is not prime and 𝑥 is written in binary}
={𝑥|𝑥 = 𝑦𝑧 for integers 𝑦,𝑧>1, 𝑥 in binary}
𝐶𝑂𝑀𝑃𝑂𝑆𝐼𝑇𝐸𝑆 ∈ NP

Intuition直观 for P and NP
P:可以快速测试成员资格的所有语言 All languages where can test membership quickly
NP:可以快速验证成员资格的所有语言 All languages where can verify membership quickly
可满足性问题 Satisfiability Problem
Defn:
1.一个布尔公式𝜙有着布尔变量(TRUE,FALSE)以及布尔操作(AND (∧), OR (∨), and NOT (¬) )
2.𝜙是可满足性的,如果𝜙被赋值为 True 对于一些变量的赋值评估
3.令𝜙 = (x∨y)∧(¬x∨¬y),则𝜙是可满足的
4.𝑆𝐴𝑇∈P → P = NP
多项式时间可归约性
Defn:
A对B 是 多项式时间可归约的(A <= $_p$B) 如果 A<= $_m$B 对于一个可在多项式时间内计算的归约函数
也就是说: 如果 A <= $_p$B 并且 𝐵 ∈ P ,则 A ∈ P
Lecture10 NP 完全性
EXPTIME
Defn: EXPTIME =$⋃_𝑘$ TIME((2^𝑛)^𝑘))
= Exponential time decidable languages
= 指数时间可判定语言
NP ⊆ EXPTIME
我们不知道NP是否包含在较小的确定性时间复杂度类中
<= $_p$ Example: 3SAT and CLIQUE
Defn:
文字literal :是个布尔变量或者布尔变量的非
子句clause :是由∨连接起来的若干文字,比如(x∨x1∨x2)
一个布尔公式如果是由∧ 连接的若干文字组成,则是合取范式的Conjunctive Normal Form (CNF) ,称它为3cnf公式
3𝑆𝐴𝑇= {<𝜙>|𝜙 is a satisfiable 3CNF formula}
3𝑆𝐴𝑇= {<𝜙>|𝜙 是可满足的3cnf公式}
Them:3SAT <= $_p$CLIQUE
(证明见书)
NP完全性的定义
Defn: B是NP完全的,如果B满足:
1.𝐵 ∈ NP
2.对所有的𝐴∈NP,A<= $_p$B
If 𝐵 is NP-complete and 𝐵∈P then P = NP.
如果B是NP完全的,并且有𝐵∈P,那么P = NP
库克列文定理:SAT是NP完全的
NP完全性的重要性:
1.显示为NP完全是计算难处理性的证据
2.给出一个很好的证明 P != NP 的思路

Them:HAMPATH 是 NP-完全的
(证明见书)
Construction of 𝐺
见书
Lecture11 空间复杂度
介绍
Defn:
令 f:ℕ→ℕ 这里有 f(n) >= n. 如果M 总是能停止,并且使用最多 f(n)的tape cell , 则认为TM M 在所有的长度为n的输入中,在空间f(n)内运行
Say TM M runs in space f(n) if M always halts and uses at most f(n) tape cells on all inputs of length n .
时间复杂度和空间复杂度的关系 Relationships between Time and SPACE Complexity
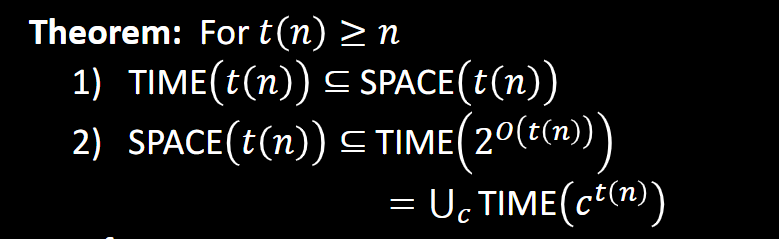
证明:
1.一个图灵机 在 t(n)步内无法使用超过 t(n)个 tape cell
2.一个图灵机 使用t(n)个 tape cells 的时候无法在不使用重复配置或者循环的前提下,使用超过 $c^t(n)$ 时间
Corollary: P ⊆ PSPACE
Theorem: NP ⊆ PSPACE
NP ⊆ PSPACE
1.𝑆𝐴𝑇 ∈PSPACE
2.If 𝐴 <= $_P$𝐵 and 𝐵∈PSPACE,then 𝐴∈PSPACE

TQBF 问题
Defn:
一个量化布尔公式quantified Boolean formula (QBF) 是一种具有leading exists ∃𝑥 存在和for all (∀𝑥) 所有量词的布尔公式。所有的变量都必须在量词规定的范围内
一个QBF 是 True 或者 False 的
Defn:
TQBF = {<𝜙>|𝜙 is a QBF that is True}
Them: 𝑇𝑄𝐵𝐹 ∈ PSPACE
𝑇𝑄𝐵𝐹 ∈ SPACE(𝑛)
Lecture12 PSPACE 完全性
概念
我们认为B是PSPACE完全的,如果它满足:
1.𝐵∈PSPACE
2.For all 𝐴∈PSPACE, 𝐴<= $_p$𝐵
If 𝐵 is PSPACE-complete and 𝐵∈P then P=PSPACE
TQBF is PSPACE-complete

N and NL
这部分主要是例子和证明,建议直接看书,重点于:
-Geography game
-𝐺𝐺 is PSPACE-complete
-Log space
-NL properties





