Lecture 9 Recursion&DP

递归 Recursion

简介

我们把一个调用它自己的方法称为递归
当我们想要且可以比较简单地“把复杂问题分解为简单问题”的时候，就可以使用它

递归的关键在于两个部分，一个是最对重复问题的分解与解答，而另一个就是“停下”的操作，即Base Case

递归不断调用自身，直到达到基本情况Base Case，然后再一步步调用回来，得到答案

递归与效率

递归实现往往非常简单
对最初初几次调用非常快
对于较大的值，程序在输出之间暂停的时间惊人地长
（结果表明，使用递归计算斐波那契数非常糟糕）

方法需要很长时间，因为每个级别都会使递归调用的数量增加一倍

递归可以简化代码，但并不总是有效

也就是说，我们不希望递归经常调用自身，如果我们想在调用次数不呈指数增长的条件下使用递归，我们可以使用动态规划

动态规划 Dynamic Programming

简介

动态规划（也称为动态优化）是一种解决复杂问题的方法
它将复杂问题分解为一组更简单的子问题，只解决每个子问题一次，然后存储它们的解，这样自然就解决了“为了某个值不得不重复调用”的弊端

为了确定问题是否可以通过应用动态规划解决，我们检查两个地方：
1.该问题涉及需要反复解决的重叠子问题。在动态规划中，我们只解决这些子问题一次，并将其存储起来以备将来使用
2.如果一个大问题可以用子问题的解来解决，那么我们说这个问题也有一个最优子结构性质

实例

优化Fibonacci Series

我们尝试来修改Fibonacci Series的算法如下：
我们利用自底向上的解法来解决与存储它：

1
2
3
4
5
6
7
8
9
10
public int fibBU(int x) {
    int fib[] = new int[x + 1];
    fib[0] = 1;
    fib[1] = 1;
    for (int i = 2; i < x + 1; i++) {
        fib[i] = fib[i - 1] + fib[i - 2];
        //这里利用了一个数组来存储已经计算过的fib数值
    }
    return fib[x];
}

利用自上向下的推导来得到答案，这和我们之前的写法一样，但是加入了检查是否已经算过某个数的步骤进行优化：

1
2
3
4
5
6
7
8
9
10
public int fibTD(int n) {
    if(n == 0) return 1;
    if(n == 1) return 1;
    if(fib[n] != 0) {
        return fib[n];
    }else {
        fib[n] = fibTD(n-1) + fibTD(n-2);
        return fib[n];
    }
}

递归的二分查找

二分查找懂得都懂，这里不赘述了 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private int recFind(long searchKey, int lowerBound, int upperBound) {
    int middle;
    middle = (lowerBound + upperBound ) / 2;
    if(a[middle] == searchKey) 
        return middle; //找到结果
    else if(lowerBound > upperBound){
        return -1; // lowerBound > upperBound 意味着我们已经都搜索一遍了，此时还没找到的话就是不存在
    } else { 
        //如果还没搜索完就更新区域然后再寻找    
        if(a[middle] < searchKey) 
            return recFind(searchKey, middle+1, upperBound);////如果我们要找的值在较大部分
        else 
            return recFind(searchKey, lowerBound, middle-1); //如果我们要找的值在较小部分
    } 
}

这里利用递归的二分查找，是 分治法 divide and conquer approach 的一个例子

分治：把大问题分成两个小问题，每个小问题单独解决，然后将它们分成更小的问题
该过程一直持续,直到到达基本情况

汉诺塔

递归中的一个很经典的问题，这里就不描述问题了

加入我们利用递归来解决它，那么大概的思维是：
0.把问题分解成越来越小的子树
1.将顶部n-1个磁盘的子树从源控制棒移动到中间棒
2.将剩余的最大磁盘从源棒移动到目标棒
3.解决将子树从中间杆移动到目标杆的问题(递归)
4.继续调用递归算法来移动较小的子树
5.而当我们只是移动一层时，则不需要其他操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class TowersApp {
    static int nDisks = 3;
    public static void main(String[] args) {
        doTowers(nDisks, 'A', 'B', 'C');
    }

    public static void doTowers(int topN, char src, char inter, char dest) {
        if(topN == 1) 
            System.out.println("Disk 1 from " + src + " to "+ dest);
        else {
            doTowers(topN-1, src, dest, inter); // src to inter
            System.out.println("Disk " + topN +  " from " + src + " to "+ dest);
            // move bottom
            doTowers(topN-1, inter, src, dest); // inter to dest
        }
    }
}

其它问题，如回文检查，幂运算等，这里就不赘述了，原理是一样的

归并排序 MergeSort

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用

在排序时，它的思想是：将数组分成两半，然后对每一半进行排序
(两半的大小不一定要相同)
在将两个数组合并到一个独立的工作区之前，每一次都比较每一半的最低的数
也许语言的解释比较拗口，不过来张图就非常简单明了了：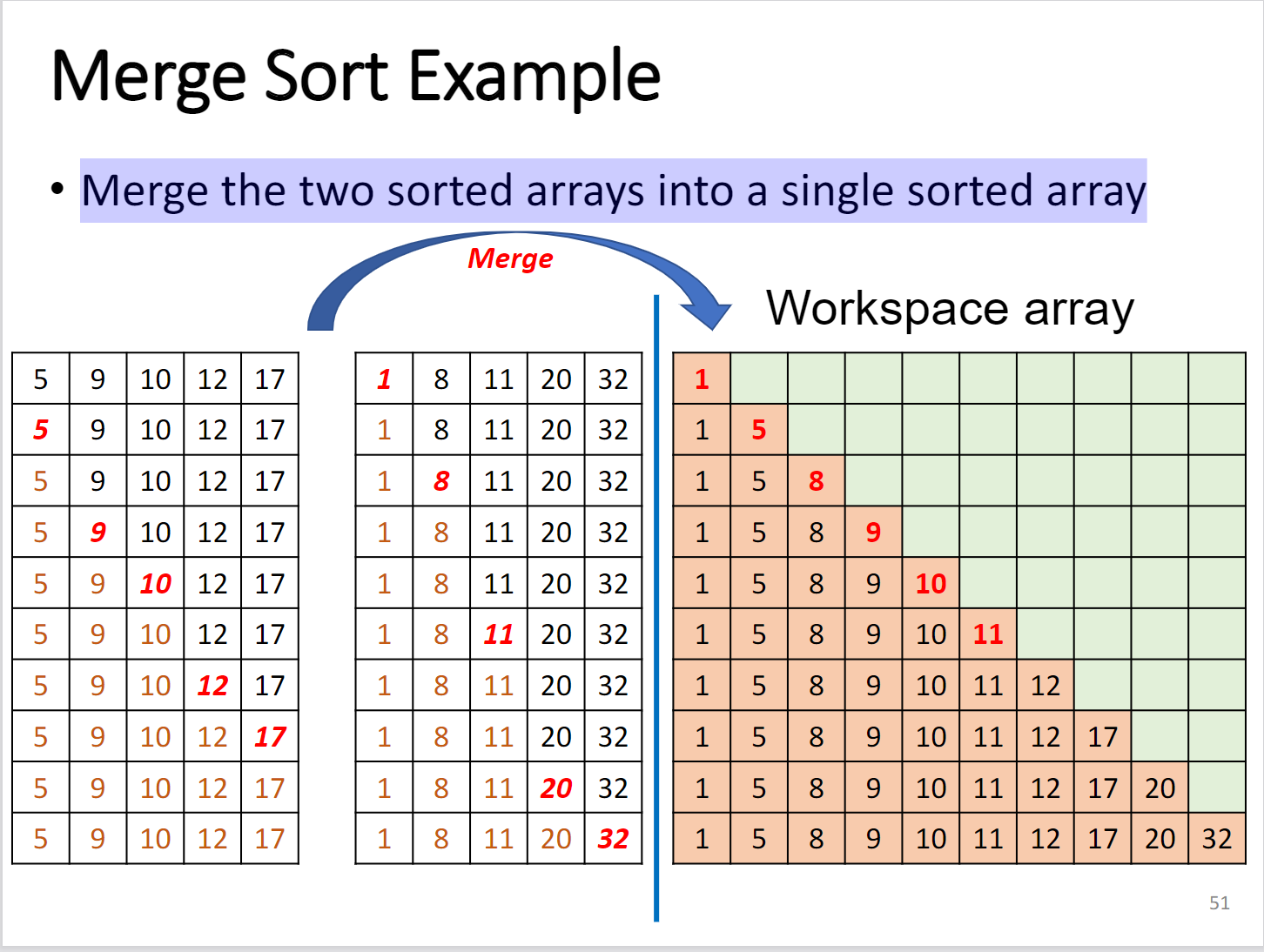

归并排序Java实现(迭代)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public void merge(long[] workSpace, int first, int second, int upperBound) {
    int j = 0; // workspace index
    int lowerBound = first;
    int mid = second - 1;
    int n = upperBound-lowerBound+1; // # of items
    while(first <= mid && second <= upperBound){
        if( theArray[first] < theArray[second] )
        workSpace[j++] = theArray[first++];
    } else{
        workSpace[j++] = theArray[second++];
    }

    while(first <= mid) //check first half for remaining
        workSpace[j++] = theArray[first++];
    while(second <= upperBound) //check second half for remaining
        workSpace[j++] = theArray[second++];
    for(j = 0; j<n; j++)
        theArray[lowerBound+j] = workSpace[j]; //copy the workspace back
} // end merge()

这样会把数组的两个工作区域合并到一个工作区域中
我们可以用一个临时区域来存储结果，如果还要后续操作的话，把这个临时数组复制回去

上文提到，我们是比较两半的最小值来进行挑选的，那如果分开的两半是未排序的呢？难不成还要去排序一下再用归并排序吗？
当然不是，我们只要不断对半分，最终只会得到一个仅有一个数字的数组，这样就简单了————于是想到利用递归
(先用图表达一下想法)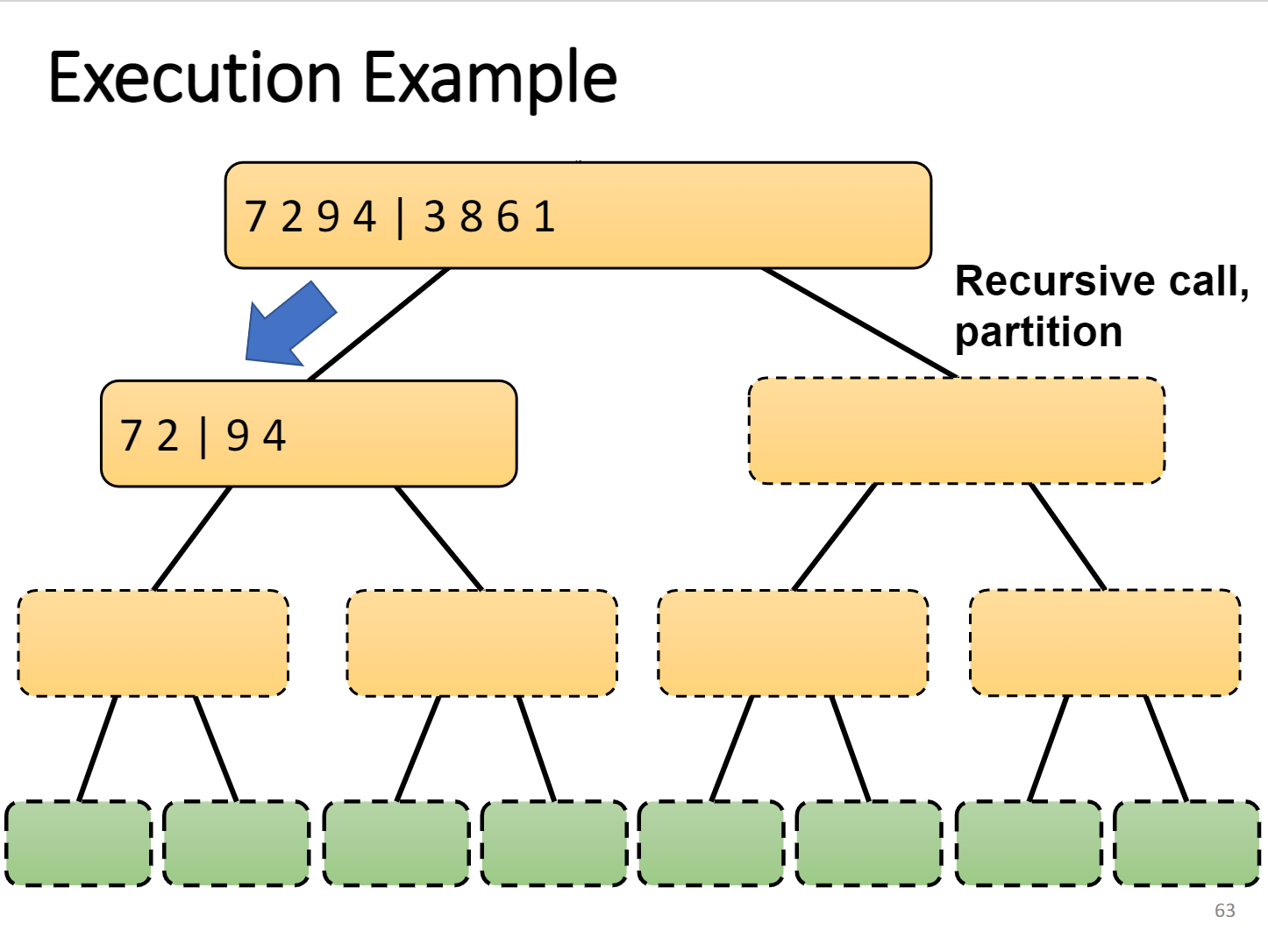

归并排序Java实现(递归)

1
2
3
4
5
6
7
8
9
10
11
12
public void recMergeSort(long[] workSpace, int lowerBound, int upperBound) {
    if(lowerBound == upperBound){
        //若数组大小为一，此时就是BaseCase,于是不用排序
        return; 
    }else { 
        //找到终点
        int mid = (lowerBound+upperBound) / 2; // sort low half
        recMergeSort(workSpace, lowerBound, mid); // sort high half
        recMergeSort(workSpace, mid+1, upperBound); // merge them
        merge(workSpace, lowerBound, mid+1, upperBound);
    }
}

或者可以参照leetCode的这题辅助理解:

合并链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

题解
十分简单粗暴，我们比较两个链表头的大小即可。
两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        } else if (l2 == null) {
            return l1;
        } else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

小结

归并测试和选择测试的比较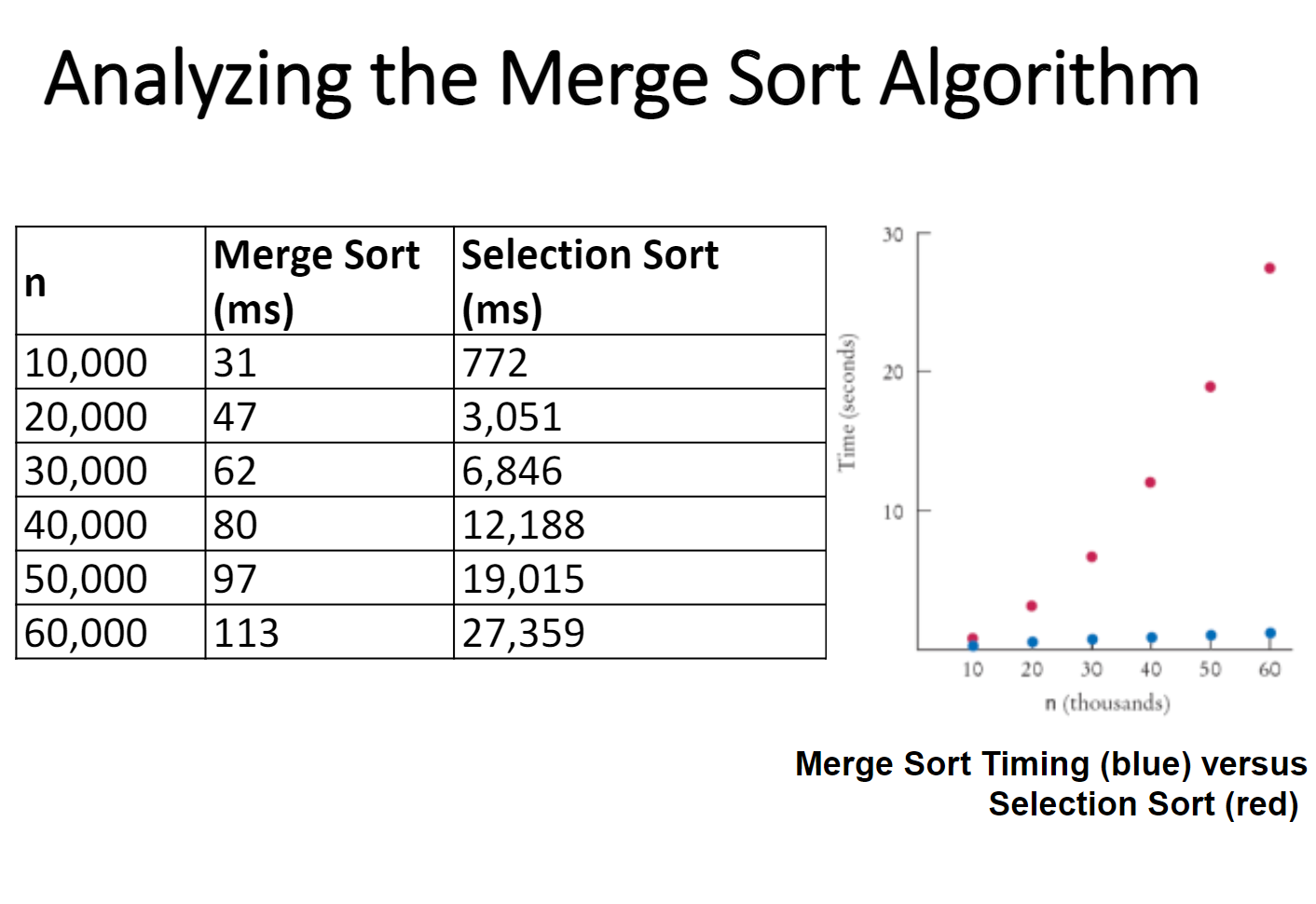

1.合并时，需要的最大比较次数比合并的项目少1 也就是 n-1
2.最小的比较数目是合并项目数的一半 也就是 n/2

Lecture 10 BitManipulation

位运算

十-十六 进制

在计算机中，十六进制是一种常见的系统。它的0-9同十进制，除此以外：
A,B,C,D,E,F 分别表示10,11,12,13,14,15

比如9A3是
$916^2$ $= 2304$
$1016^1$ $= 160$
$3*16^0$ $= 3$
则有9A3的十进制表达为 2304+160+3= 2467

在Java中…

在Java，int被32位所表示，这意味着它的范围处于 -2,147,483,648 到 2,147,483,647

位运算操作

在Java中，我们支持以下的位运算操作：
与AND ： &
或OR ： |
异或XOR： ^ (相同0，不同1)

特殊位运算

左移位 Bitwise left shift << :
取数，转换为位形式，将位左移，右边的空格填0

实例如
it result = 15 << 3
此时 15的二进制为
15 = 00000000 00000000 00000000 00001111

<< 3 代表左移三位，后续补0，则有
00000000 00000000 00000000 01111000

得到结果为 15<<3 = 120

向右有符号移动 Bitwise signed right shift >> :
取数，转换为位形式，将位右移，且：
如果原始为正数，则用0填充左边空位
如果原始为负数，则用1填充左边空位 

1
2
3
4
5
6
7
8
int result = 116 >> 3;
•116 = 00000000 00000000 00000000 01110100
•116 >>3 = 00000000 00000000 00000000 00001110
•116 >>3 = 14 which is (around 116 / 23)
int result = -116 >> 3;
•-116 = 11111111 11111111 11111111 10001100
•-116 >>3 = 11111111 11111111 11111111 11110001
•-116 >>3 = -15 which is (around -116 / 23)

向右无符号移动 Bitwise unsigned right shift >> :
取数，转换为位形式，将位右移，无论原始情况如何，都用0来填充空位 

1
2
3
4
5
6
7
8
int result = 116 >>> 3;
• 116 = 00000000 00000000 00000000 01110100
• 116 >>>3 = 00000000 00000000 00000000 00001110
• 116 >>>3 = 14 which is (around 116 / 23)
int result = -116 >> 3;
• -116 = 11111111 11111111 11111111 10001100
• -116 >>>3 = 00011111 11111111 11111111 11110001
• -116 >>>3 = 536,870,897

按位补码 Bitwise complement ~ :
取数，转换为位形式，每1翻转为0，反之亦然 

1
2
3
4
int result = ~116;
•116 = 00000000 00000000 00000000 01110100
•~116 = 11111111 11111111 11111111 10001011
•~116 = -117

其它

若 A & B == 0
这意味着 A 和 B 无论在哪个位置，都不会有相同的二进制数(否则二者与的结果会有1)

因此， ((n & (n-1)) == 0) 检查 n 是否是 2 的幂，若为真，则证明n是2的幂

不使用 +、-、* 或 / 将两个数字相加：

1
2
3
4
5
6
7
8
9
public int addition(int a, int b) {
    if(b==0) {
        return a;
    } else {
        sum = a^b;
        carry = (a&b)<<1;
        return addition(sum,carry);
    }
}