cs210算法与数据结构(一)
CS210 lecture1
概述
在此,我们将学习“存储信息的有效结构” 和 “操作信息的便捷算法”,简单来说,就是学习数据结构和算法
预告
将包含以下四个主要部分:
Recursion递归
Data structures 数据结构
Algorithms算法
Analysis of algorithms算法分析
算法:A step-by-step procedure for solving a problem via a computational process 通过计算过程逐步解决问题的过程
阿兰-图灵终于在20世纪30年代成功地为 “算法 “提供了一个全面的定义:一个可以在图灵机上运行的程序
An algorithm is:1.A well-defined, step-by-step procedure 2.That is guaranteed to terminate
程序:An implementation of an algorithm in some programming languages 一种算法在某些编程语言中的实现
数据结构:A conceptual system for organizing the data needed to solve some problems 组织解决一些问题所需数据的概念系统
What is a data structure?
数据结构是组织信息的概念结构
换句话说,我们将学习使用不同的结构来存储数据
What is an algorithm?
一种算法是一种精确的逐步踏板,用于使用有限序列来解决问题
-一个明确界定的、逐步进行的程序
-保证能够终止
Analysis of algorithms : 分析可以告诉你一个算法的运行速度,以及它将需要多少空间
算法就像你的想法,程序就是它的实现
Lecture2-Programming Revision
该部分MD作为一些知识的补充
变量 Variable
变量是内存中某个位置的名称 Variable is a name for a location in memory
变量分为两种变量:
1.原始变量Primitive :比如int和double,它们通常是小写字母
2.引用变量Reference :比如对象Object,它们通常以大写字母开头
我们可以在声明的时候给予变量一个初始值,当一个变量没有被初始化时。该变量的值是未定义的
范围和垃圾回收 Scope & garbage collection
在成员方法 member function 内定义的变量是该函数的局部变量
最明显的就是for循环,里面定义的变量i,它的life time只存在于该函数中
1 | for(int i = 0 ; i<50 ; i++){ |
当我们的函数退出(或超出范围)时,局部变量就被销毁(garbage collected)
程序员不用担心”为范围外的对象/变量取消分配内存”这件事
不像C和C++
赋值 Assignment
赋值语句更改变量的值,使用=操作符
a = 33 ;
我们已经做过多次这种事情了,它正规的定义就是:对右边的表达式求值,结果存储到左侧变量中
原始变量Primitive Types (基本/初始变量)
在Java中有八大初始变量:
byte,short,int,long,float,double,char,boolean
Bits And Bytes
Bit:一个bit就是1或0(真或假),本质就是一个标志开关的旗子
Bype:一个byte以8个bit组成,比如:10110011
1 Kilobyte kb= about 1,000 bytes (1,024 to be precise)
1 Megabyte mb= about 1,000,000 bytes (1,024 * 1,024)
1 Gigabyte gb= about 1,000,000,000 bytes
在原始变量中,其大小如下:
int: -21474836482147483647,大小为4bytes127,大小为1byte
byte:-128
short:-3276832767,大小为2bytes9,223,372,036,854,775,807,大小为8bytes
long:–9,223,372,036,854,775,808
double: +-$10^308$ ,有效小数约为15位,8bytes
float: +-$10^38$ , 有效小数约为7位,4bytes
char:字符类型,表示Unicode编码方案中的代码单位,2bytes
boolean:判断正负,1bit
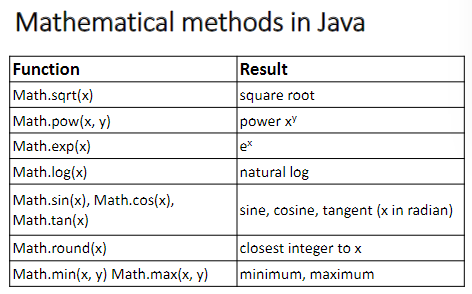
Math Class
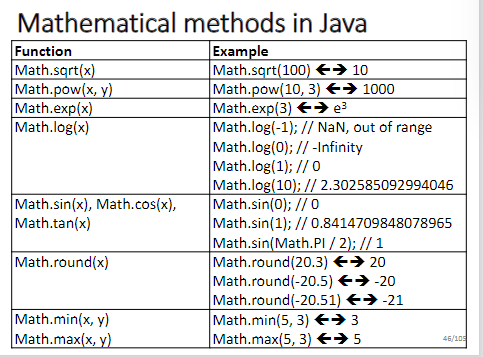
Math.round()
会把浮点数转换为最近的整数
Math.round( 11.5)= 12
Math.round(-11.5)= -11
Math.round( 11.46)= 11
Math.round(-11.46)= -11
Math.pow(x,y) Math.sqrt(x)
Math.pow(x,y) x的y次方
Math.sqrt(x) 根号x
其它
Math.exp(x) $e^x$
Math.log(x)natural log
Math.sin(x), Math.cos(x), Math.tan(x) sine, cosine, tangent (x in radian)
Math.min(x, y),Math.max(x, y) minimum, maximum
操作符
i++ ++i
我们int i = 1 ;
i++ 先赋值再运算,比如对于 a = i++ , 我们先进行a = i 计算,再运行i=i+1,最终所得是 a==1
++i 则是先运算再赋值,对于a = ++i , 我们先进行 i = i+1,再进行a = i ,得到 a == 2
(–同理)
数学运算
字符串
使用==比较字符的时候
上述测试旨在查看两个字符串变量是否引用同一个字符串对象
比较字符串使用 s1.equals(s2)
使用s1.compareTo(s2)的时候,会按照字典顺序来比较二者的值
If s1.compareTo(s2) < 0 then the string s1 comes before the string s2 in the dictionary
Lecture3 Methods and Objects
Lecture4 Arrays and Array Algorithms
String API
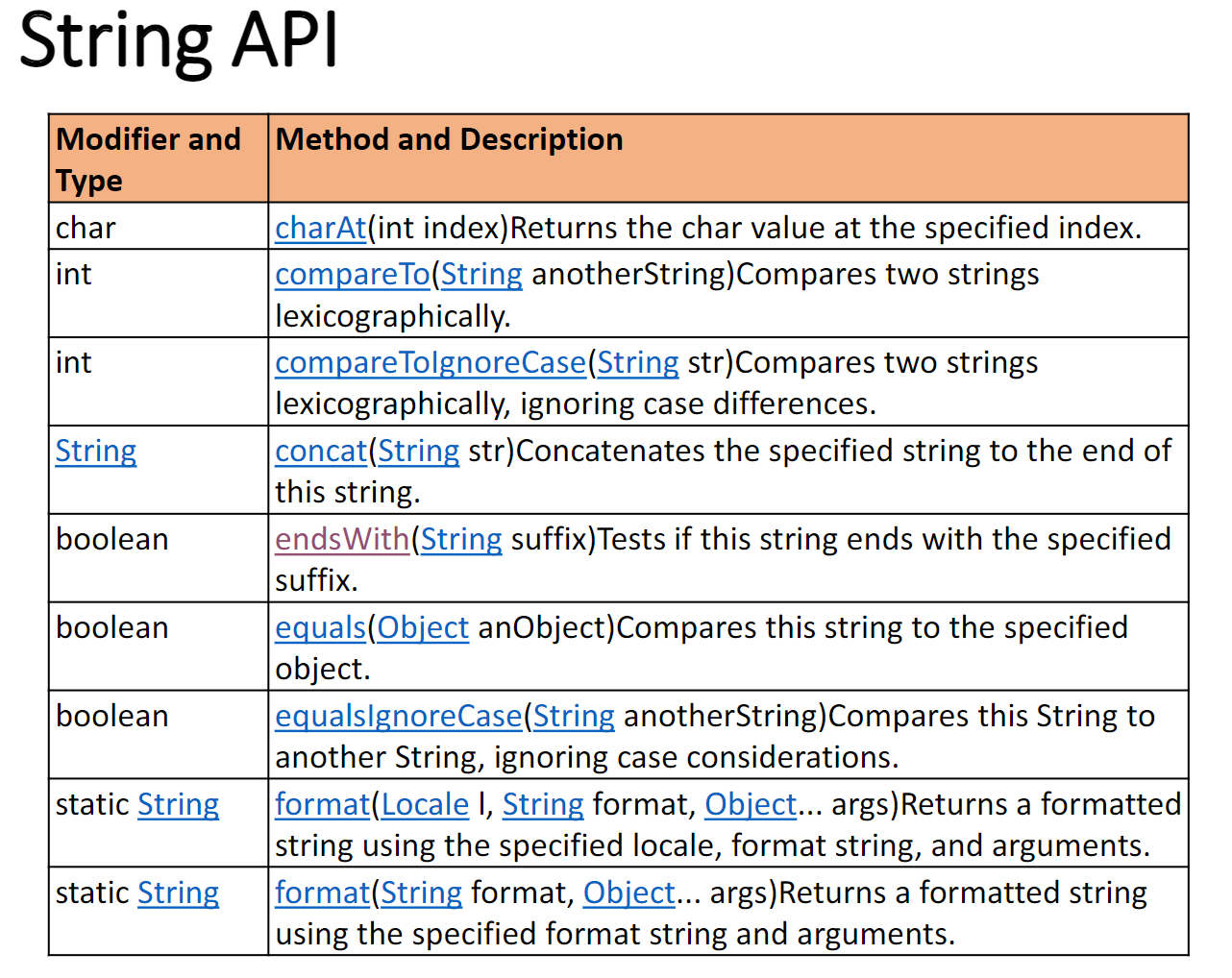
修饰符
public:它是public,这意味着它可以从任何地方运行
static:它是静态的,这意味着您不需要创建对象就可以使用它
void:它不会返回一个结果
另外,Java程序可以接受字符串数组作为输入参数(String[]args)
abstract: Abstract是一个抽象方法为空的类(没有与这些方法相关联的代码),它不能被实例化
final:表示了一个不能有子类的类
public:描述可以由任何其他包实例化或扩展的类
没有修饰符,则类是友好的 friendly(只能由同一包中的类实例化)
方法
普通方法称为实例方法,因为它们对对象的特定实例进行操作
要使用这些方法,首先需要创建类的对象,然后调用该对象上的方法
而静态方法static methond可以在不创建对象的情况下自行运行
Random
Math.random() 提供大于等于0小于1的随机数
生成的随机数的返回值为double
Eratosthenes筛选获得素数
1.创建一个布尔数组,其大小与你要检查的数字范围相一致
2.从2开始,将所有值设置为true
3.从插槽2中的元素开始,检查该插槽中的值是否为真–如果不是,则跳过它并转到下一个数字
4.现在循环数组的其余部分,并将插槽号为该插槽号倍数的每个元素设置为“false”
5.完成后,任何仍包含’true’的插槽必须是素数
补充
封装 encapsulation
封装隐藏了所有不重要的细节
创建数组时,根据数组类型初始化所有值:
•数字:0
•布尔值:false
•对象引用:null
二维数组: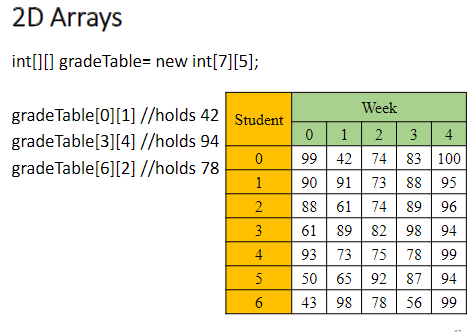
Math.random()提供>=0和<1的随机数
Lecture 5
这部分建议还是看书理解
计算法
使用大O的时候只关心最高项
O(n):运行时间增加的速度与大小增加的速度成正比
O(n^2):运行时间的增加与问题规模的平方成正比
O(1):运行时间为常数
O(logN):时间以对数大小的速率缓慢增加
程序计算大O
无论问题的大小如何,都运行相同次数的语句只是常量
您所感兴趣的只是增加循环的大小,循环的迭代次数是怎么增加的
单个循环运行 n 次表示O(n)
每个运行 n 次的嵌套循环表示O(n^2)
注意观察运行的次数,而不是只看循环有几个嵌套
Lecture6
三种排序算法
它们的复杂度都是$O(n^2)$
冒泡排序 Bubble Sort
从数组的开头开始
比较前两个数字
如果左边的一个更大,则将其与右边的一个交换
向右移动一个位置并检查接下来的两个•继续这样做直到到达数组的末尾
最大的数字现在已经“冒泡”到顶部
回到开头,重复上述的流程进行排序
在数组的顶部停止,就可以得到结果
示意图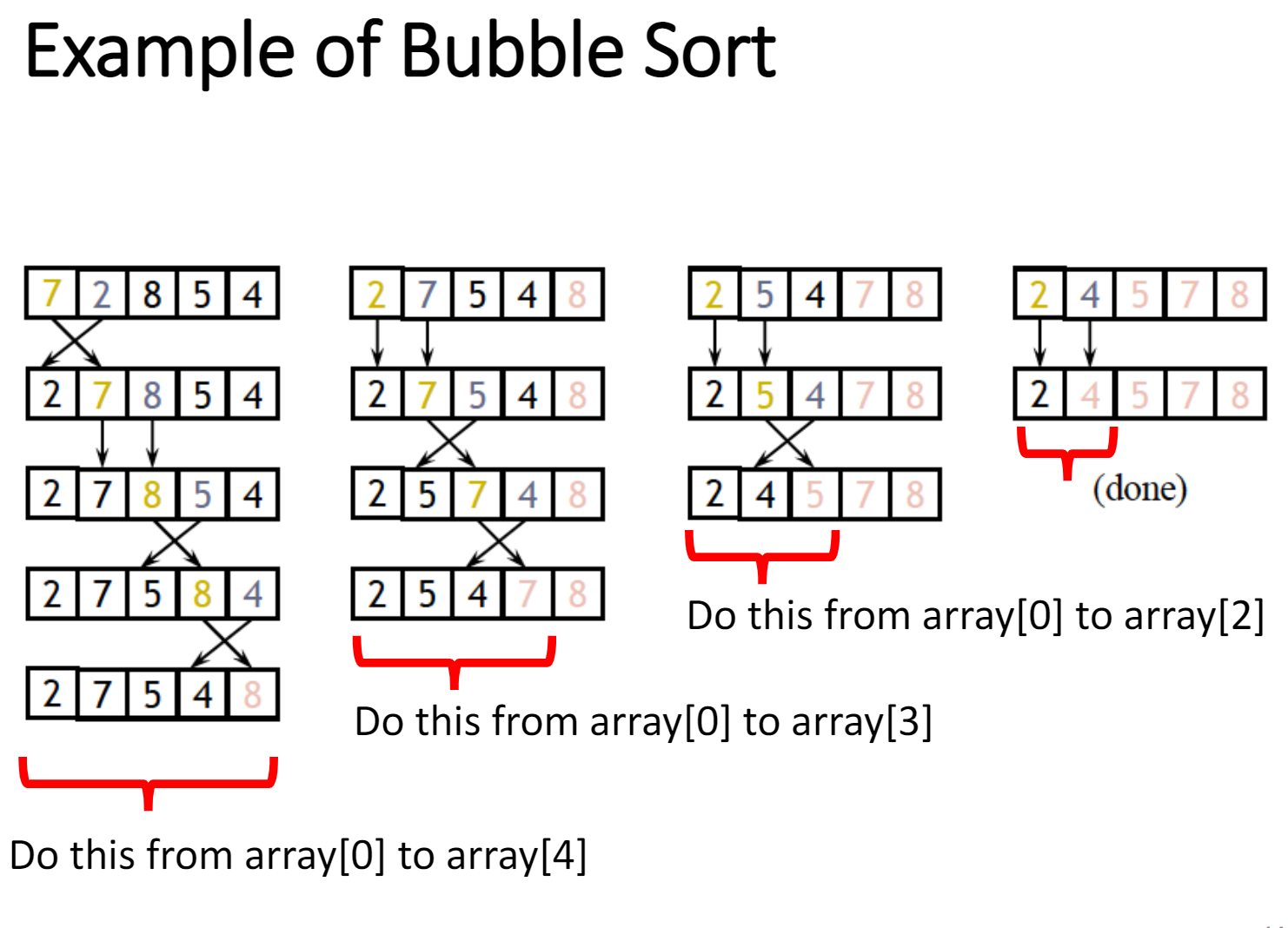
代码实现
选择排序 Selection Sort
选择排序优化了交换的流程,虽然它的复杂度依旧是$O(n^2)$
但在一般情况下,它能够拥有比冒泡算法更短的运行时间
原因在于,在每一次”冒泡”中,我们都找到了某个最值,但在之后的计算中,我们依旧对它进行了比较
这导致我们花费了本不应该花费的时间
于是,我们可以随着冒泡外循环的进行,减少外循环检查的范围
优化示意图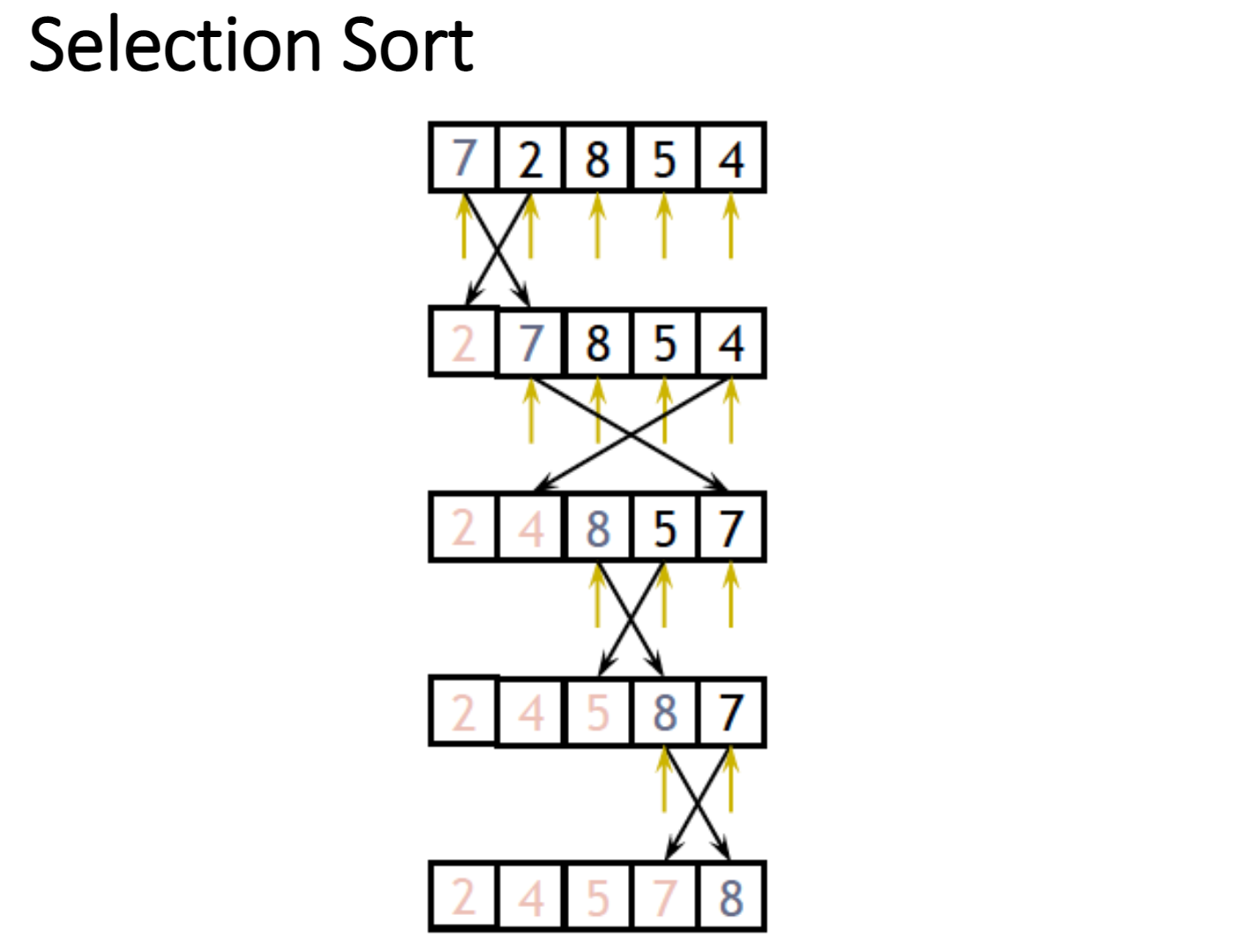
红色是已找到最值(这里是最小值)
蓝色是当前计算的对象
黄色是当前排序的范围
代码实现
插入排序 Insertion Sort
虽然复杂度还是$O(n^2)$,但是速度比前三种更快
一般而言,我们会把插入排序用在其它排序法的最后阶段,比如快速排序
在快速排序中,我们不再使用交换,而是将元素向上移动来“腾出空间”
其核心思想在于把已经排序好的数放在左侧
示意图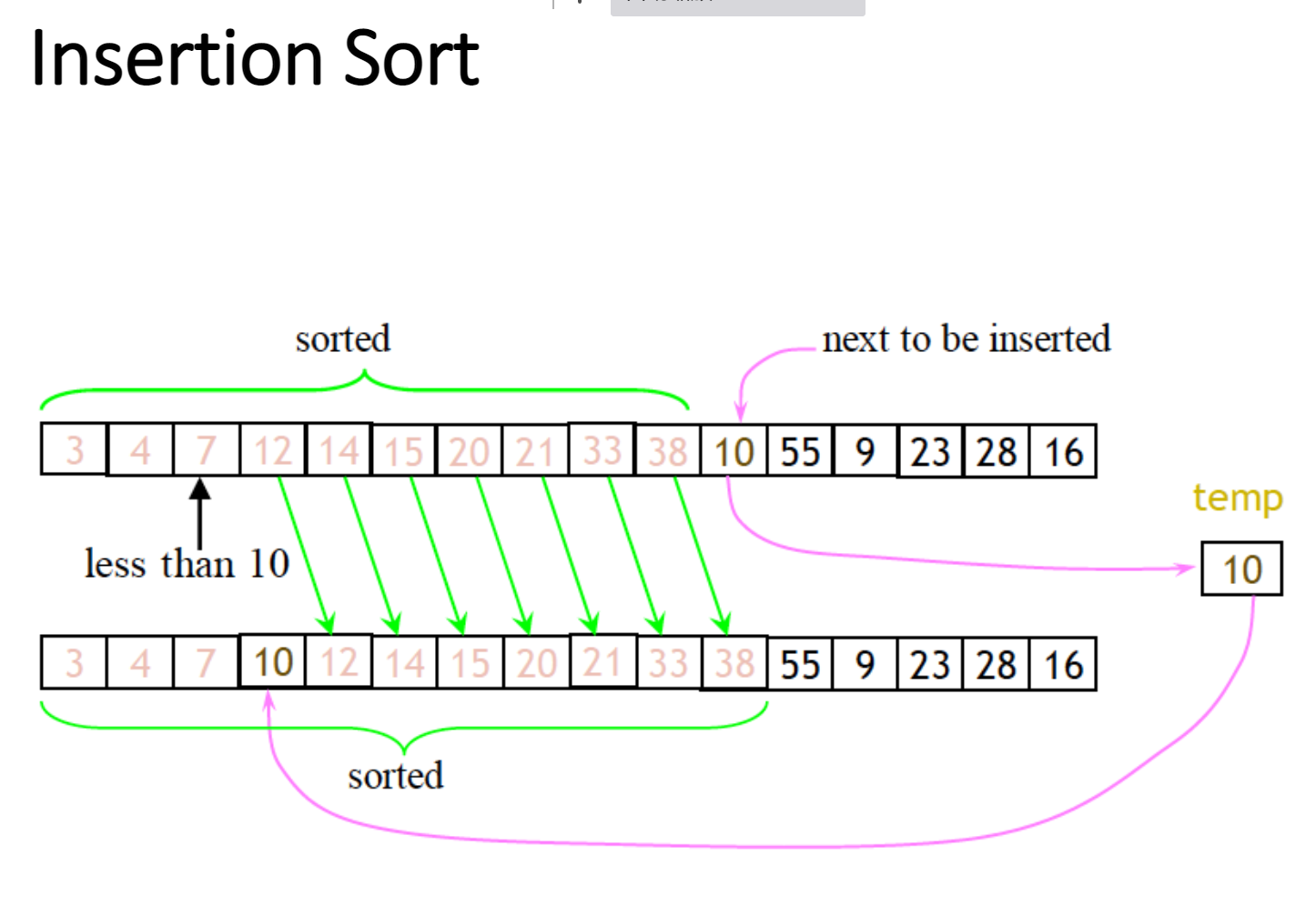
部分待排序列表(黑色)最初只包含列表中的第一个元素
每次迭代都会从“尚未检查订单”输入数据中删除一个元素(红色)
然后会使用这个元素到左侧区域比较大小
最终插入到排序列表中
代码实现
对于逆序排列的数据,运行速度不会比冒泡排序快
小结
冒泡排序
通过每次交换将最大的冒泡到末尾
选择排序
选择最小值并将该元素交换到开头
插入排序
查找元素应在排序部分中的位置并将所有元素向上移动到腾出空间
三者的复杂度都是&O(n^2)$





